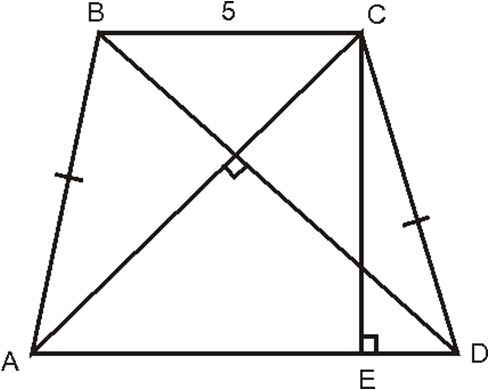
ABCD-трапеция,AD=15.Найти CE

Ответ:

10 единиц

Объяснение:

Воспользуемся данным рисунком. Пусть диагонали равнобедренной трапеции ABCD  пересекаются в точке О и по условию они взаимно перпендикулярны( AC ⊥ BD).Рассмотрим треугольник  BOC - прямоугольный  , т.к. диагонали пересекаются под прямым углом и равнобедренный , т. к. трапеция равнобедренная .  ∠ OBC=∠ OCB  = 45° , BO= OC = BC sin45° =

5..

Аналогично Δ AOD -прямоугольный и равнобедренный . ∠OAD = ∠ODA = 45°. AO= DO = AD sin 45° = .

Рассмотрим Δ ACE прямоугольный, в нем ∠ CAE =45° , тогда∠ACE = 45° и Δ ACE равнобедренный ( т.к. два угла равны).

AC = AO+ OC; AC= .  Тогда CE=AE = AC·sin45° = единиц.

Если в равнобедренной трапеции диагонали взаимно перпендикулярны, то её высота равна средней линии данной трапеции, то есть равна полусумме оснований ⇒ СЕ = (BC + AD)/2 = (5 + 15)/2 = 10

Ответ: 10