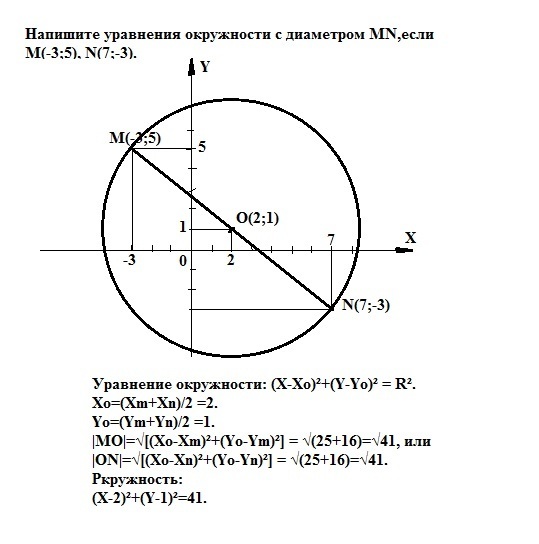
Напишите уравнения окружности с диаметром MN,если M(-3;5), N(7;-3)
Объяните пожалуйста подробно, а то на уроке не присутстврвала :(

Если диаметр - отрезок MN, то середина О этого отрезка - центр окружности.Найдем координаты центра:Xo=(Xm+Xn)/2 = (-3+7)/2=2.Yo=(Ym+Yn)/2 = (5+(-3))/2=1.Радиус окружности равен длине (модулю) отрезка MO илиотрезка ON:|MO|=√[(Xo-Xm)²+(Yo-Ym)²] = √[(2-(-3))²+(1-5)²] = √(25+16)=√41.  Или|ON|=√[(Xn-Xo)²+(Yn-Yo)²] = √[(7-2)²+(-3-1)²] = √(25+16)=√41.Уравнение окружности:(X-Xo)²+(Y-Yo)²=R²  или в нашем случае:(X-2)²+(Y-1)²=41.