Задать вопрос Регистрация
Помочь другим

  • ПОМОГИТЕ, ПОЖАЛУЙСТА, РЕШИТЬ ЗАДАЧКУ ПО ГЕОМЕТРИИ!!!!! БУДУ ОЧЕНЬ БЛАГОДАРНА)
    смотр. фото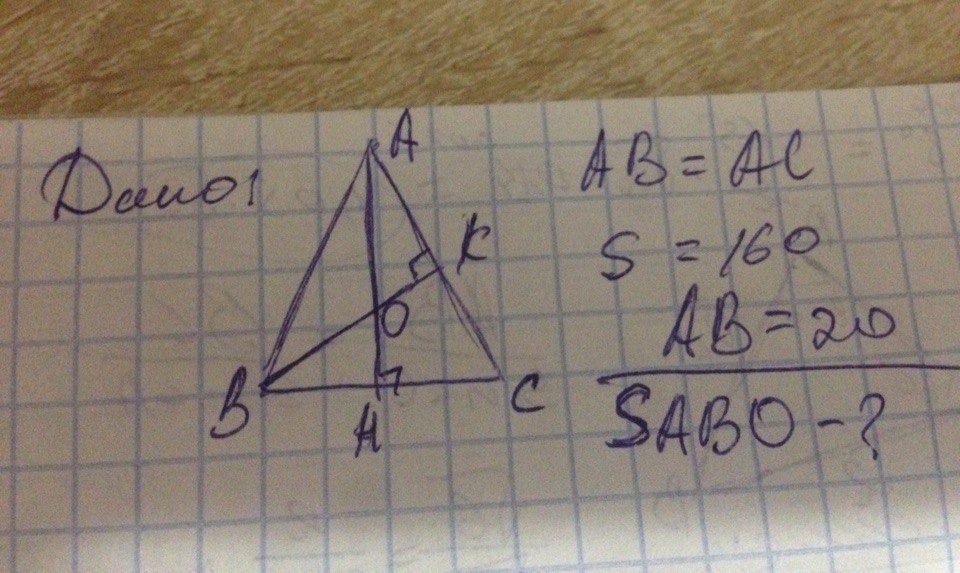

    question img

Ответы 1

  • так как AB=AC=20 => ΔBAC равнобедренный, значит AH является биссектрисой и медианой и высотой(свойство равнобедренного треугольника)BK - высота => AK=(1/2)*AC=(1/2)*20=10.по формуле площади треугольника:SΔBAC=(1/2)*AB*AC*sin(A)(1/2)*20*20*sin(A)=160sin(A)= \frac{160}{200} = \frac{16}{20} = \frac{4}{5} рассмотрим ΔAKB - он прямоугольный( угол BKA=90°).так как AO - биссектриса, то угол BAO=1/2 угла Aнайдем синус BAOвоспользуемся формулой синуса половинного угла и основным тригонометрическим тождеством:sin^2\frac{A}{2} = \frac{1-cosA}{2} \\cos^2A=1-sin^2A=1- \frac{16}{25} = \frac{9}{25} \\cosA= \frac{3}{5} \\sin \frac{A}{2} =\sqrt{ \frac{1- \frac{3}{5} }{2} }=\sqrt{ \frac{ \frac{2}{5} }{ 2 } }=\sqrt{ \frac{1}{5}}= \frac{\sqrt{5}}{5} sin(BAO)=sin \frac{A}{2} =\frac{\sqrt{5}}{5}рассмотрим ΔAKB - в нем AO - биссектриса. Для определения биссектрисы в прямоугольном треугольнике есть формула:AO=AK*\sqrt{ \frac{2*AB}{AK+AB} } \\AK=10 \\AB=20 \\AO=10*\sqrt{ \frac{40}{30} }= \frac{20}{\sqrt{3}} = \frac{20\sqrt{3}}{3} теперь можно найти площадь ΔABO:SΔABO=(1/2)*AB*AO*sin(BAO) AB=20 \\AO= \frac{20\sqrt{3}}{3} \\sin(BAO)= \frac{\sqrt{5}}{5} \\S\Delta ABO= \frac{1}{2} *20*\frac{20\sqrt{3}}{3}*\frac{\sqrt{5}}{5}= \frac{20*20\sqrt{3}*\sqrt{5}}{3*5*2} = \frac{40\sqrt{15}}{3}Ответ: \frac{40\sqrt{15}}{3}

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years