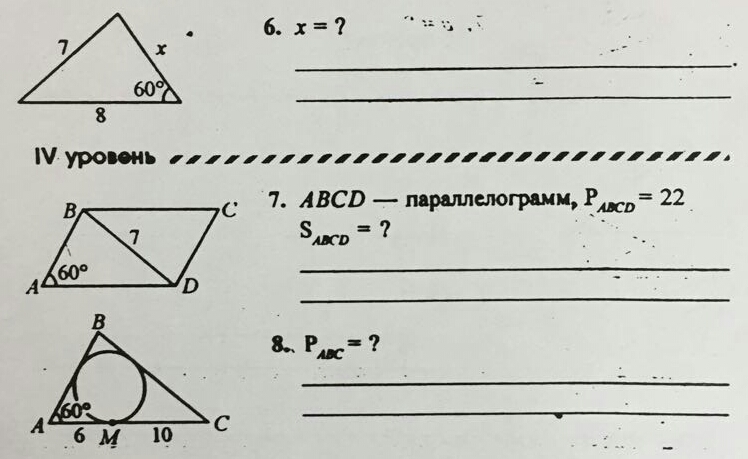
Геометрия, 9 класс. Используя теорему косинусов, решите задачи.

1) 49=64+х²-2*x*8cos60°°49=64+x²-2*x*8*(1/2)x²-8x+15=0x₁=5, x₂=3Ответ: 5 или 32)Пусть одна сторона равна a, а другая b, тогдаP=2*(a+b);  22=2*(a+b);  a+b=11;  b=11-aПо теореме косинусов:49=a²+(11-a)²-2*a*(11-a)*cos6049=a²+121-22a+a²-11a+a₂3a²-33a+72=0a²-11a+24=0a₁=8 a₂=3b₁=11-8=3;  b₂=11-3=8Получим две пары сторон 8 и 3, или 3 и 8S=a*b*sin60=3*8*=Ответ 12√33) Пусть точка Е точка касания окружности и стороны АВ, точка Т точка касания окружности и стороны ВС, тогда по свойству касательных отрезков имеем, АМ=АЕ=6; ЕВ=ВТ=х; ТС=СМ=10, по теореме косинусов имеем.(x+10)²=16²+(x+6)²-2*16*(x+6)cos60x²+20x+100=256+x²+12x+36-16x-9620x-12x+16x=256+36-96-10024x=96x=4 Значит, АМ=16;  АВ=6+4=10;  ВС=4+10=14Тогда P=AM+AB+BC=16+10+14=30Ответ: 30