-
Решите задачу
Сторона основания правильной четырёхугольной пирамиды равна 2 корня 2 дм, угол между боковым рёбром и плоскостью основания - 45 градусов. найдите высоту, боковое ребро и площадь боковой поверхности пирамиды.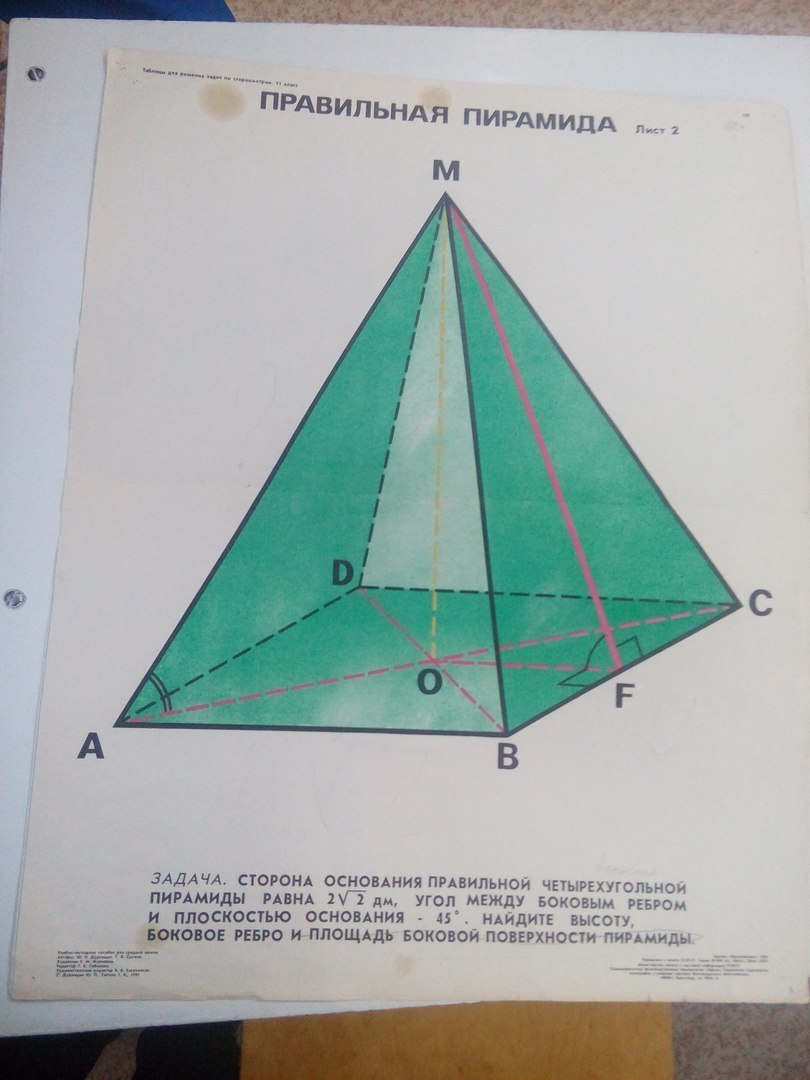
Ответы 1
-
В основании - квадрат со стороной 2
дм.Диагональ квадрата AC = AB *
= 2
*
= 4 дм.AO = AC / 2 = 2 дмΔAMO - прямоугольный равнобедренный, высота OM = AO = 2 дм ΔAMO = ΔAOB по общему катету АО и углу 45°, поэтому боковое ребро AM = AB = 2
дм.ΔAMB - равносторонний.Площадь ΔAMВ = АВ^2 *
/ 4 = = (2
)^2 *
/4 = = 2
Площадь боковой поверхности = 4 * площадь ΔAMВ = 8
дм^2Ответ: Высота 2 дм, боковое ребро 2
дм, Площадь боковой поверхности = 8
дм^2
-
Автор:
skinnyqdp8 - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
при яких значеннях a, функція:
f(x) = (a-4)x^2 +2ax+a+2
не має жодних нулів-
Предмет:
Алгебра -
Автор:
butterelnp - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
помогите написать рассказ рассуждение на тему "Нужно ли быть старательным"
-
Предмет:
Литература -
Автор:
nathanesxh - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
Помогите преобразовать предложения в номере 13 ( а)
-
Предмет:
Немецкий язык -
Автор:
libbyvgk1 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
- 1кН=...Н 0.5кН=...Н 1.7кН=...Н 25000Н=...кН 3700Н=...кН 400Н=...кН
How much to ban the user?
1 hour
1 day
100 years
