AB=CA, E-середина Ab,F-середина CD. Доказать:OE=OF. Помогите пожалуйста , задача по геометрии для 7 класса.

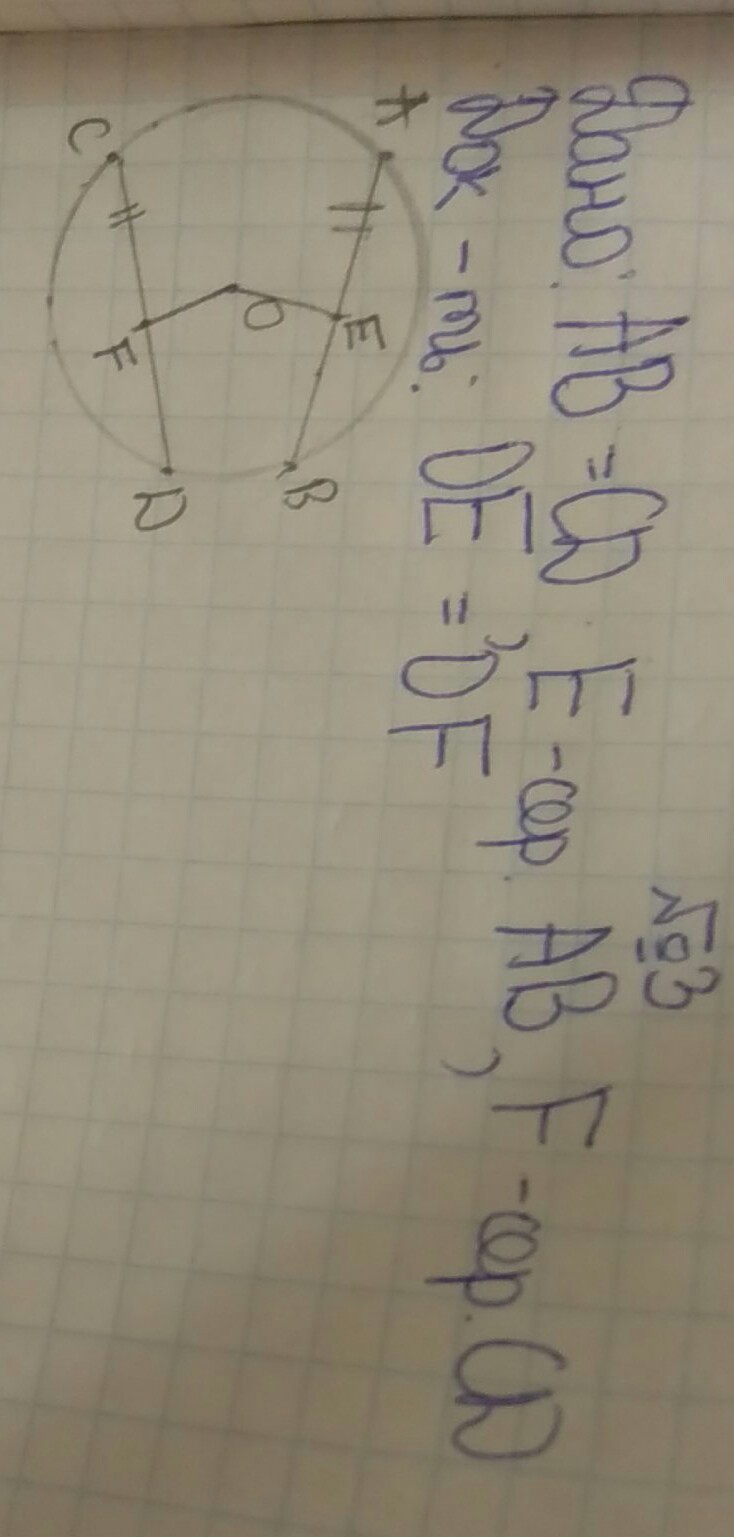
Ответ:

ОА = ОВ как радиусы, значит ΔОАВ равнобедренный.

ОЕ - его медиана, проведенная к основанию, значит является высотой, т.е. ОЕ⊥АВ.

OC = OD как радиусы, ΔOCD равнобедренный.

OF - его медиана и высота, т.е. OF⊥CD.

Рассмотрим треугольники ОАЕ и COF:

∠АЕО = ∠CFO = 90°,

ОА = ОС как радиусы,

АЕ = CF как половины равных отрезков (AB = CD по условию, а точки Е и F их середины), ⇒

ΔОАЕ = ΔOCF по катету и гипотенузе.

Значит и ОЕ = OF.