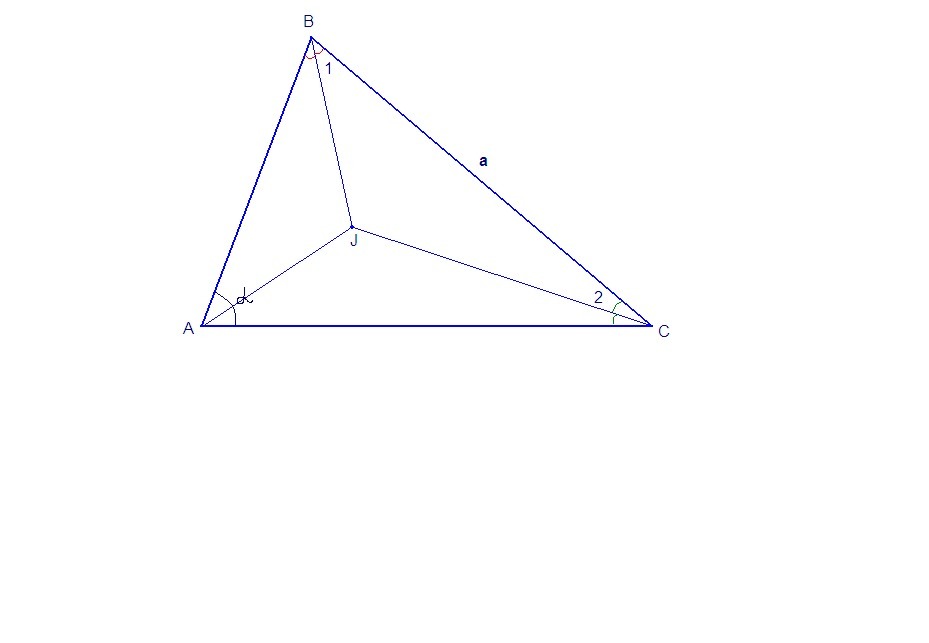
в треугольнике АВС угол А равен альфа а сторона ВС равна а, J-точка пересечения биссектрис. Найдите радиус окружности, описанной около треугольника BJC/

∠АВС + ∠АСВ = 180° - α∠1 + ∠2 = (180° - α) / 2 = 90° - α/2, так как эти углы - половинки углов АВС и АСВ.ΔBCJ: ∠BJC = 180° - (∠1 + ∠2) = 180° - (90° - α/2) = 90° + α/2По следствию из теоремы синусов отношение стороны треугольника к синусу противолежащего угла равно двум радиусам описанной окружности.Для ΔBJC:ВС / sin∠BJC = 2R2R = a / sin(90° + α/2)R = a / (2sin(90° + α/2)), по формуле приведения:R = a / (2·cos(α/2))