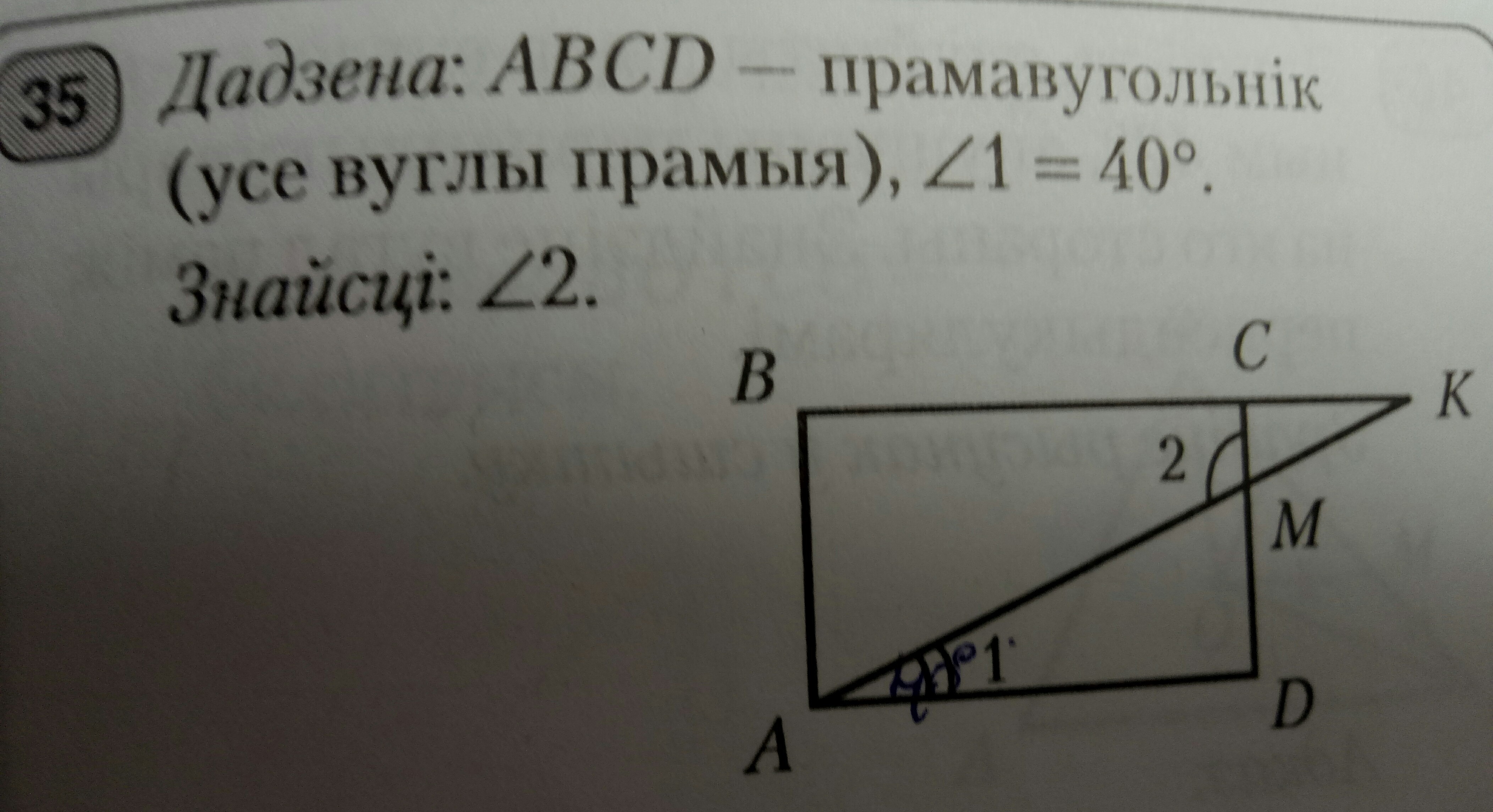
Дано ABCD прямоугольник, угол 1 равен 40 градусов. Найти угол 2

\angle 2 = 130^{\circ}

Рассмотрим 2 способа решения данной задачи:

1 способ.

Прямоугольник - это параллелограмм, у которого все углы прямые.

\Rightarrow \triangle ADM - прямоугольный, где \angle MDA - прямой.

Свойство: Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Смотрим: \angle 2 - внешний угол \triangle ADM.

Значит \angle 2 = \angle 1 + \angle MDA = 40^{\circ} + 90^{\circ} = 130^{\circ}

2 способ.

Как я уже написала в 1 способе, прямоугольник - это параллелограмм, у которого все углы прямые.

\Rightarrow BK || AD, по свойству параллелограмма.

При пересечении двух параллельных прямых секущей, накрест лежащие углы равны.

\Rightarrrow \angle1 = \angle BKA, как накрест лежащие при пересечении BK и AD секущей AK.

Сумма смежных углов равна 180^{\circ}.

Так как \angle BCD = 90^{\circ}, по свойству прямоугольника \Rightarrow смежный с ним \angle KCD = 180^{\circ} - \angle BCD = 180^{\circ} - 90^{\circ} = 90^{\circ}\\ \Rightarrow \triangle CKM -прямоугольный.

Рассмотрим \triangle CKM:

Сумма острых углов прямоугольного треугольника равна 90^{\circ}.

\angle KMC = 90^{\circ} - \angle BKA = 90^{\circ} - 40^{\circ} = 50^{\circ}\\

Сумма смежных углов равна 180^{\circ}.

\Rightarrow \angle 2 = 180^{\circ} - \angle KMC = 180^{\circ} - 50^{\circ} = 130^{\circ}