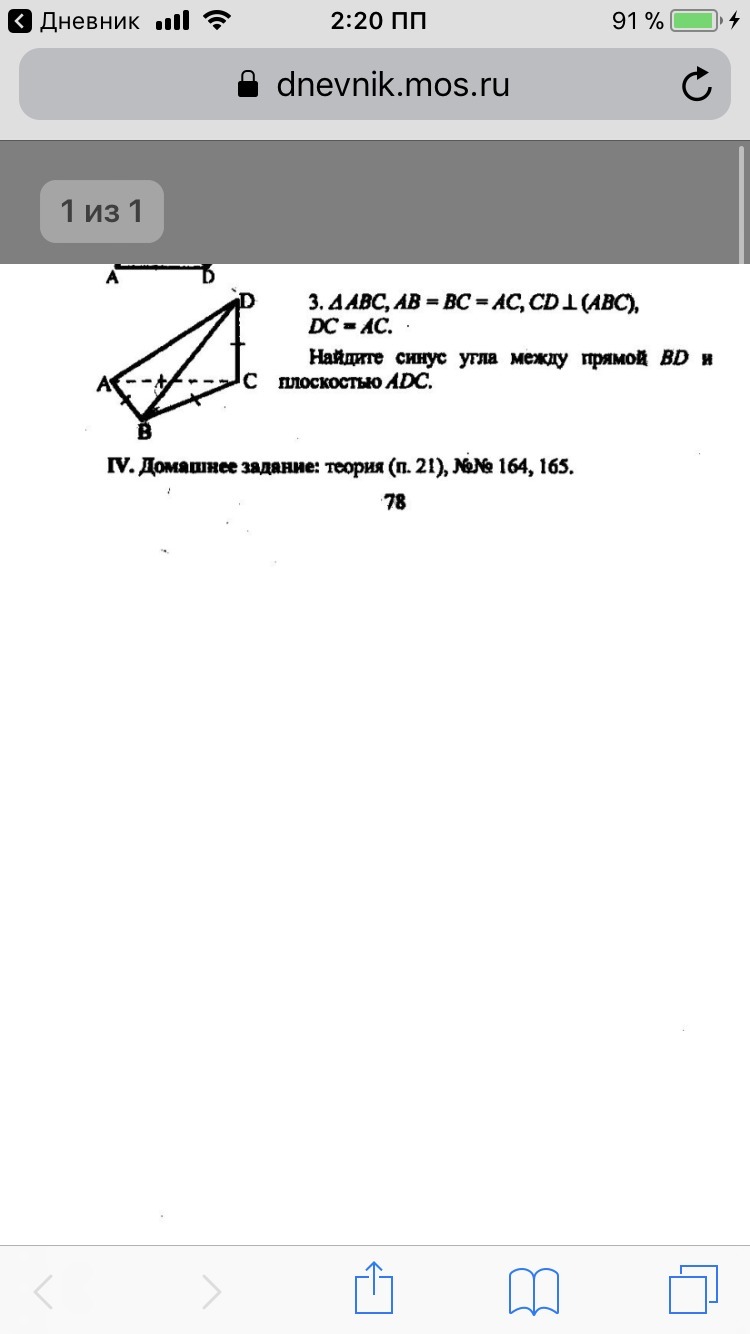
Найдите синус угла между прямой bd и плоскостью ADC. Срочно , желательно с решением , заранее спасибо!!

Ответ:

sin∠BDO = √6/4

Объяснение:

Угол между прямой и плоскостью - это угол между прямой и ее проекцией на эту плоскость.

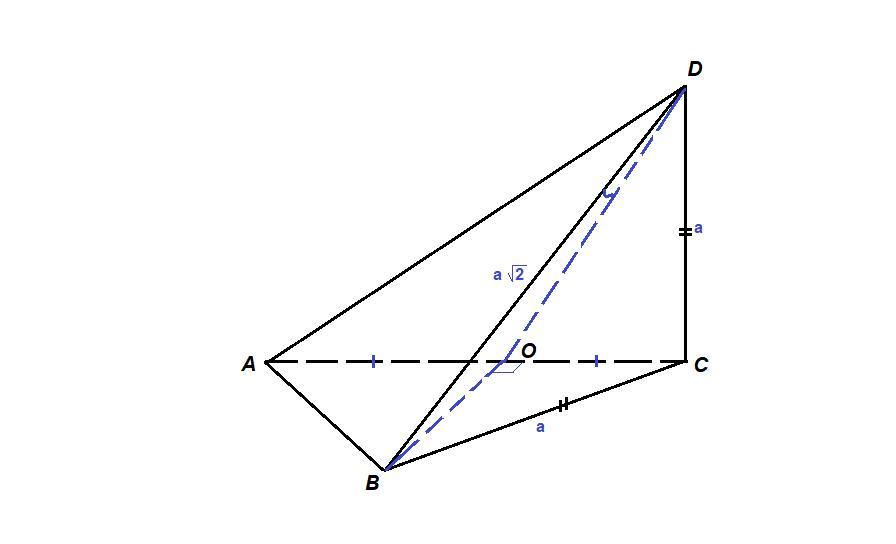
Построим проекцию прямой BD на плоскость (ADC).

Пусть О - середина АС.

ΔАВС равносторонний, значит ВО - медиана и высота,  ⇒

ВО ⊥ АС.

ВО ⊥ DC ( DC ⊥ (ABC),  BO ⊂ (ABC) )

Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна плоскости.

Значит, ВО ⊥ (ADC), тогда OD - проекция прямой BD на плоскость  (ADC).

∠BDO - это угол между прямой BD и плоскостью (ADC) - искомый.

_________________________

Пусть а - сторона ΔАВС, тогда DC = BC = a,

DB = a√2 как гипотенуза равнобедренного треугольника ΔBDC.

BO=\dfrac{a\sqrt{3}}{2} как высота равностороннего треугольника.

ΔBOD:  ∠BOD = 90°, так как ВО⊥(ADC), значит ВО перпендикулярна любой прямой этой плоскости.

sin\angle BDO=\dfrac{BO}{BD}=\dfrac{a\sqrt{3}}{2}:(a\sqrt{2})=\dfrac{\sqrt{3}}{2\sqrt{2}}=\dfrac{\sqrt{6}}{4}