-
Очень нужно решение 4 задачи.
Треугольник АВС-правильный, О- центр окружности ,вписанной в треугольник АВС, АВ=12, ОМ=4. Найти расстояние от точки М до прямой ВС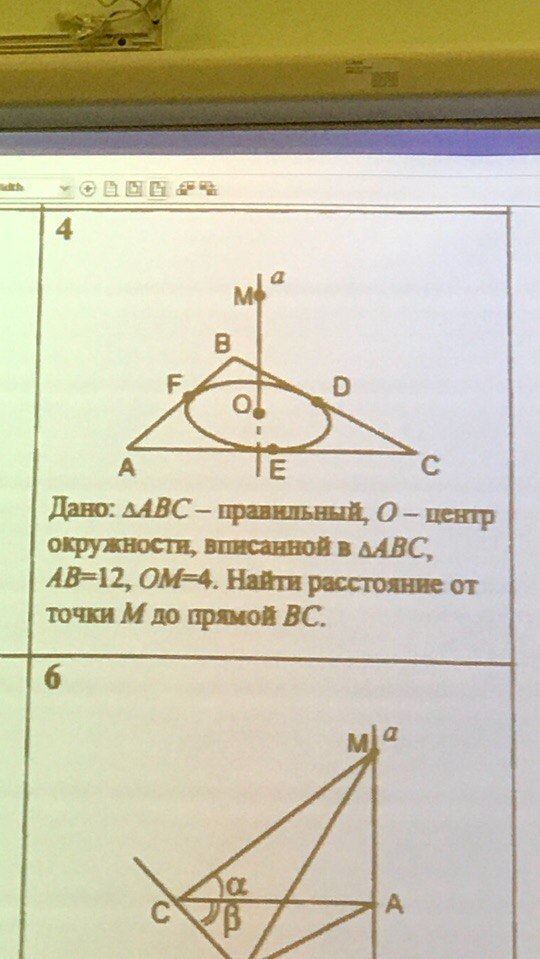
Ответы 1
-
OD⊥ВС как радиус, проведенный в точку касания.
OD - проекция MD на плоскость АВС, значит
MD⊥BC по теореме о трех перпендикулярах.
Расстояние от точки до прямой - длина перпендикуляра, опущенного из точки на прямую, значит
MD - расстояние от точки М до прямой ВС - искомое.
OD - радиус окружности, вписанной в правильный треугольник:
OD = AB√3/6 = 12√3/6 = 2√3
ΔOMD: ∠MOD = 90°, по теореме Пифагора:
MD = √(OD² + OM²) = √((2√3)² + 4²) = √(12 + 16) = √28 = 2√7
-
Автор:
hunter - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Из общей массы овощей, завезенных в магазин, 7/18 составляла свекла, 30%- морковь, а остальные 112кг-капуста. Сколько овощей завезли в магазин? (Выполните порядок действий)
-
Предмет:
Математика -
Автор:
austinrvw9 - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
о чем стихотворение зимний вечер? (в двух словах)
-
Предмет:
Литература -
Автор:
duke80 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Перечислите Какие чудеса произошли с главными героями в Ночь перед Рождеством?
-
Предмет:
Литература -
Автор:
frederick10 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
7x-(3+2x)=a+9
13-(2x-5)=x-3
3x-(10-9x)=22x
26-(17-2x)=5x решите уравнение-
Предмет:
Математика -
Автор:
valeriecastillo - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
