В правильном тетраэдре ABCD, ребро которого равно а, DO-высота тетраэдра,М-середина DO.
a)через точку М проведите сечение, параллельное плоскости ВСD. б)Найдите периметр сечения.
в)Найдите площадь сечения. г) в каком отношении плоскость сечения делит высоту тетраэдра AF,считая от А?

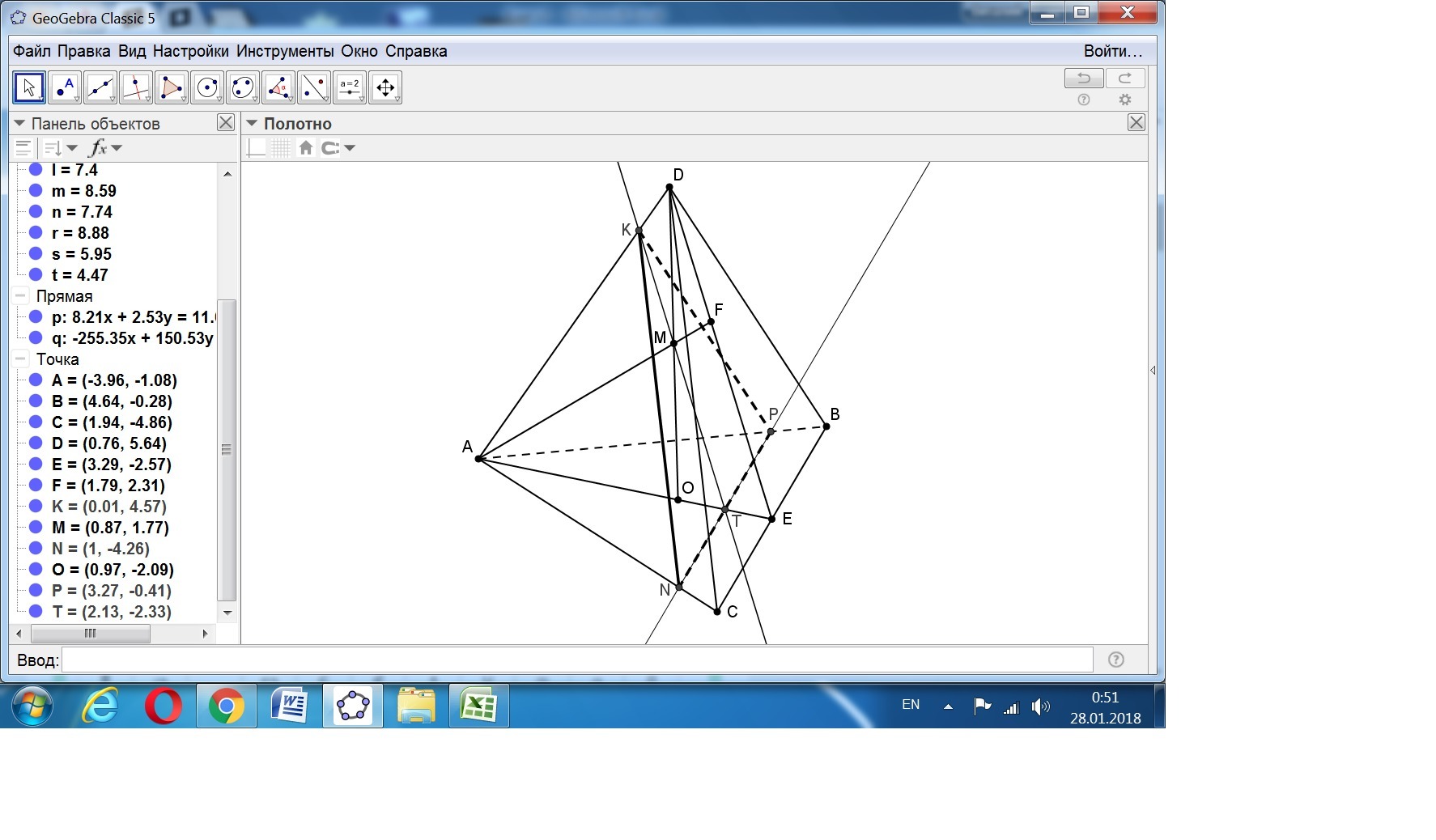
Дан правильный тетраэдр ABCD, ребро которого равно а, DO-высота тетраэдра, М-середина DO.Высота DO равна а√2/√3 (это свойство правильного тетраэдра).Точка О делит высоту АЕ основания в отношении 2:1 от вершины.АЕ = а*cos 30° = a√3/2.Тогда отрезки АО и ОЕ равны:АО = (2/3)*(a√3/2) = a√3/3, ОЕ = (1/3)*(а√3/2) = а√3/6.Примем длину МО = х.Из подобных треугольников AMO и AFE составляем пропорцию:х/АО = EF/AF.Так как EF = OE, а AF = DO, то пропорция примет вид:х/(а√3/3) = (а√3/6)/(а√2/√3).Отсюда значение х равно:х = (а√3)/(6√2) = (а√6)/12 = (а√2)/(4√3) = OD/4.Получаем ответ на вопрос - г) в каком отношении плоскость сечения делит высоту тетраэдра AF,считая от А?Ответ: DM:MO = 3:1.Сечение через точку М, параллельное плоскости ВСD, пересекает АЕ в точке Т, которая делит ОЕ пополам.Тогда АТ = (5/6)АЕ и треугольник в полученном сечении имеет коэффициент подобия к треугольнику ВСД, равный 5/6.Площадь подобного треугольника NКР в сечении равна  площади ВСД, умноженной на квадрат коэффициента подобия.S(BCD) = (1/2)BC*DE = (1/2)a*(a√3/2) = a²√3/4.S(NKP) = (a²√3/4)*(25/36) = a²*25√3/144.Периметр NКР равен (5/6)*3а = 5а/2.