Периметр прямокутного трикутника дорівнює 80 см, а катети відносяться як 8:15. Знайдіть сторони трикутника.

Ответ:

16 см, 30 см и 34 см.

Объяснение:

Периметр прямоугольного треугольника равен 80 см, а катеты относятся как 8 : 15 . Найти стороны треугольника.

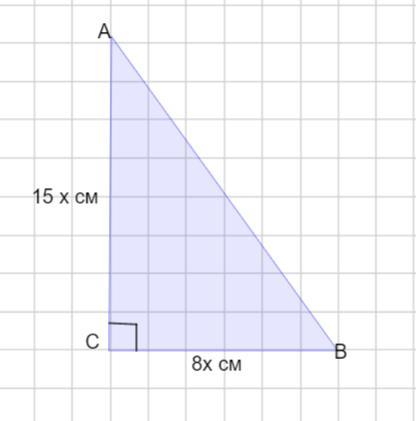
Пусть дан Δ АВС - прямоугольный. Катеты ВС: АС = 8 : 15.

Пусть ВС = 8х см, а АС = 15х см . Выразим гипотенузу АВ. Для этого воспользуемся теоремой Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

АВ²= ВС² +АС²;

АВ² = (8х)²+ (15х)²;

АВ² = 64х² +225х²;

АВ² = 289 х²

АВ =√(289х²)= 17х

Значит, гипотенуза АВ = 17х см.

Периметр треугольника  - это сумма длин всех сторон.

Р =АС +ВС +АВ

Тогда

15х +8х +17х = 80;

40х =80;

х=80:40;

х= 2

Тогда ВС = 8 · 2 = 16 см ,  АС =15 · 2 = 30 см и АВ = 17 · 2 = 34 см.

Значит, стороны треугольника 16 см, 30 см и 34 см.

#SPJ1