-
1. Смежные стороны параллелограмма равны 32 см и 28 см, а один из его
углов равен 150 градусов. Найдите площадь параллелограмма.
2. Найдите площадь ромба, если его сторона равна 40 см, а диагонали
относятся как 6:8.
3. На рисунке AB II CD.
Докажите, что AO∙OC=BO∙OD
Найдите АВ, если ВС=24 см, ОВ=9 см, СD=25 см.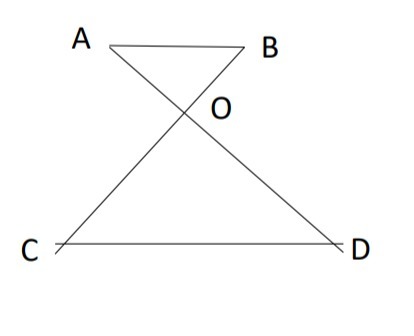
-
Предмет:
Геометрия -
Автор:
nestlebullock - 6 лет назад
-
Ответы 1
-
1. Назовем прямоугольник АВСD, в котором AB=CD=28 см, BC=AD=32 см, угол B=150 градусам.Если угол B равен 150 градусам, то угол А равен 180-150=30 градусам.Проведем высоту BH к стороне AD. Рассмотрим треугольник ABH. В нем угол А=30 градусам, а угол AHB=90 градусам. Тогда сторона, лежащая против угла в 30 градусов, равна половине гипотенузы, т.е. BH=AB/2=28/2=14 см.S=BH*AD=14*32=448 см²2. Рассмотрим любой из треугольников, на которые ромб делят диагонали. Он прямоугольный(по свойству ромба), а еще в нем катеты(половины диагоналей) тоже относятся как 6:8(или 3:4), гипотенуза равна 40.Обозначу за 3x один катет, за 4x другой катет. По теореме Пифагора:(3x)²+(4x)²=40²16x²+9x²=160025x²=1600x²=64x=8; 3x=24; 4x=32.Тогда длины диагоналей равны 24*2=48 см и 32*2=64 см.Площадь ромба равна половине произведения его диагоналей.S=48*64/2=48*32=1536 см².3)а)Треугольники AOB и DOC подобны(∠AOB=∠DOC как вертикальные, ∠ABO=∠DCO как накрест лежащие). Тогда AO/DO=BO/CO.По свойству пропорций, АО*СО=BO*DO, что и требовалось доказать.б)Если ВС=24 см, ОВ=9 см, СD=25 см, то CO=24-9=15 см.k(коэффициент подобия)=BO/CO=9/15=3/5=0,6.АB=k*CD=0,6*25=15 cм.
-
Автор:
trey437 - 2 года назад
-
16
-
-
Добавить свой ответ
Еще вопросы
-
можно ли в примере сократить 6 a в кубе и 6a ?
-
Предмет:
Математика -
Автор:
urbano - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Приведите примеры дискуссии, софистики ,полемики, эклектики
-
Предмет:
Русский язык -
Автор:
monicaqonx - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Помогите, пожалуйста!!! cos 7pi/6-sin 4pi/3
-
Предмет:
Алгебра -
Автор:
adánrodriguez - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
[tex]63x - 13.7 = 13(0.1 + 5x)[/tex]
-
Предмет:
Математика -
Автор:
mayravrbv - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
