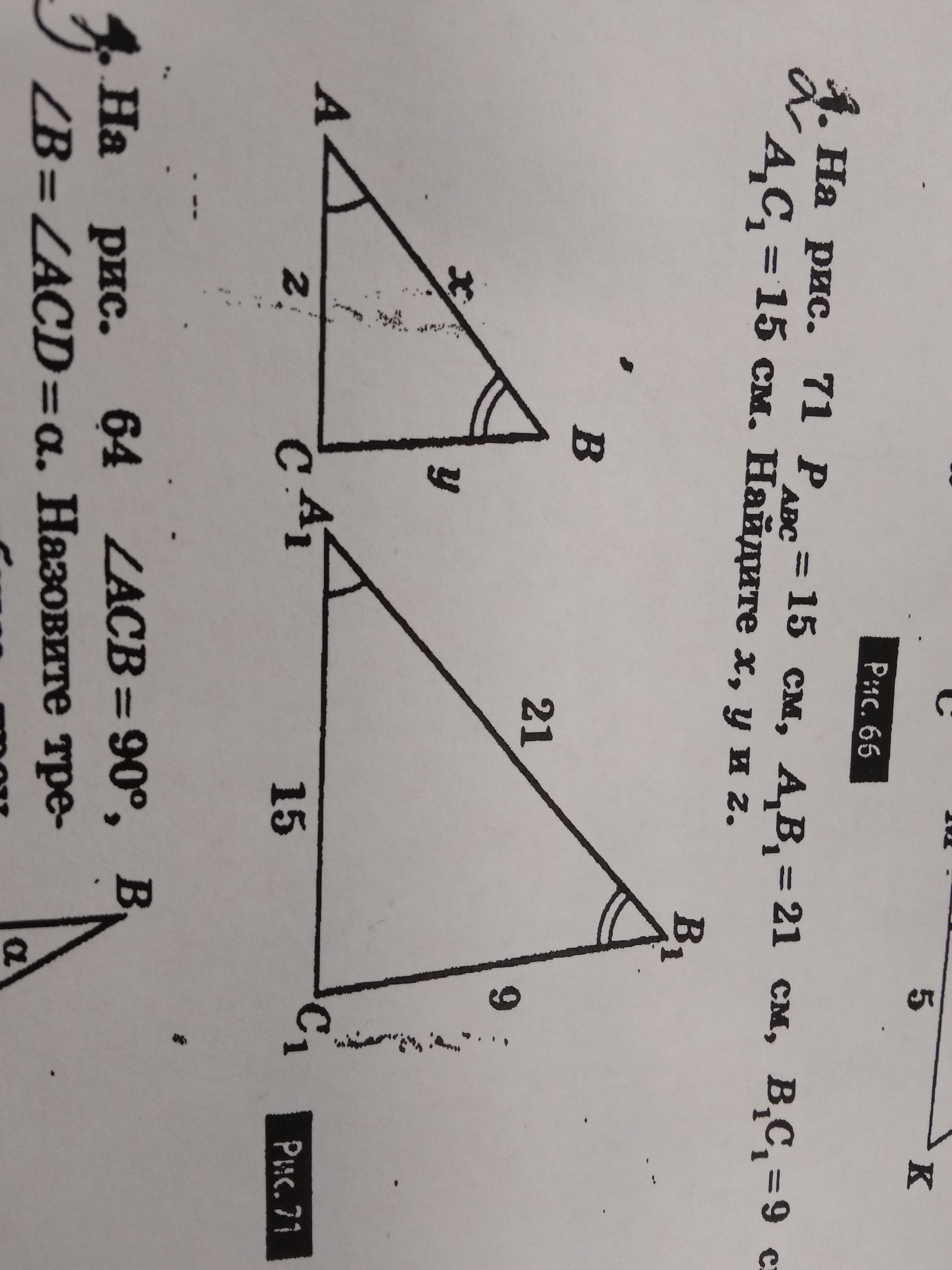
На рис. 71 Pabc=15см, A1B1=21см, B1C1=9см, A1C1=15см. Найдите x,y и z.

Дано :

ΔАВС и ΔА₁В₁С₁.

∠А = ∠А₁.

∠В = ∠В₁.

Р(ΔАВС) = 15 (см).

А₁В₁ = 21 (см).

В₁С₁ = 9 (см).

А₁С₁ = 15 (см).

Найти :

х = ?

у = ?

z = ?

Решение :

• Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны (первый признак подобия треугольников).

Так как -

∠А = ∠А₁

∠В = ∠В₁

То -

ΔАВС ~ ΔА₁В₁С₁ по первому признаку подобия треугольников.

• Периметры подобных треугольников относятся как коэффициент подобия.

Найдём Р(ΔА₁В₁С₁) -

Р(ΔА₁В₁С₁) = А₁В₁ + В₁С₁ + А₁С₁ = 21 (см) + 9 (см) + 15 (см) = 45 (см).

Тогда по выше сказанному -

\frac{P(\triangle A_{1}B_{1}C_{1} ) }{P(\triangle ABC)} = k \\\\\frac{45}{15} = k \\\\\boxed{k = 3}

Внимание! Так как в числителе был периметр бóльшего треугольника, то и в дальнейшем мы будем ставить в числитель стороны бóльшего треугольника.

• Отношения сходственных сторон подобных треугольников (сторон, лежащих напротив равных углов в подобных треугольниках) равно коэффициенту подобия.

То есть -

\frac{A_{1}B_{1} }{AB} = \frac{B_{1}C_{1} }{BC} = \frac{A_{1}C_{1} }{AC} = k

- - -

\frac{A_{1}B_{1} }{AB} = k\\\\\frac{21 }{x} = 3\\\\3x = 21\\\\x = 7

x = 7 (cм).

- - -

\frac{B_{1} C_{1} }{BC} = k\\\\\frac{9}{y} = 3\\\\3y = 9\\\\y = 3

y = 3 (cм).

- - -

\frac{A_{1}C_{1} }{AC} = k\\\\\frac{15 }{z} = 3\\\\3z = 15\\\\ z = 5

z = 5 (см).

Ответ :

7 (см), 3 (см), 5 (см).