-
Срочно! Прошу! Решите с объяснением! Найди область значений для:
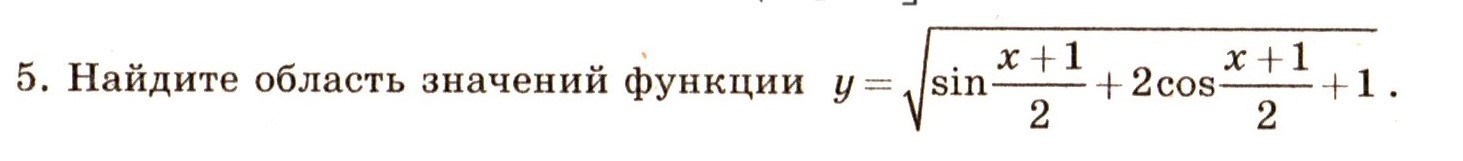
Ответы 1
-
W=sin((x+1)/2)+2*cos((x+1)/2)= √5 *( (1/√5*sin((x+1)/2) + (2/√5)*cos((x+1)/2) ), т.к. ( (1/√5)^2 + (2/√5)^2 = (1/5)+(4/5) = 1.то существует такой угол φ, что cos(φ)=(1/√5), и sin(φ) = (2/√5), тогдаW = √5 *( sin((x+1)/2)*cos(φ) + cos((x+1)/2)*sin(φ) ) = √5 *sin( (x+1)/2 +φ),φ - константа и φ=arcsin(2/√5).таким образом подкоренное выражение = √5 *sin( (x+1)/2 +φ) + 1,-1<=sin( (x+1)/2 + φ) <= 1-√5 <=√5*sin( (x+1)/2 +φ) <= √5,1- √5<=√5*sin( (x+1)/2 +φ) + 1 <= 1+√5 1-√5 <0,а функция f(t) = √t, определена лишь для t>=0, поэтому все такие икс, что√5*sin( (x+1)/2 +φ) + 1 < 0, не входят в область определения исходной функции, тогда мы рассматриваем √5 *sin( (x+1)/2 +φ)+1 >=0, поэтому0<=√5 *sin( (x+1)/2 +φ) +1 <= 1+√5функция f(t) = √t, строго возрастающая, значит большему значению аргумента соответствует большее значение этой функции, поэтому√0 <= √ (√5*sin( (x+1)/2 +φ) +1) <= √(1+√5);то есть 0<=y<=√(1+√5)Искомая область значений функции y есть [0; √(1+√5)].
-
Автор:
chi chicarlson - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Нужно поставить в каждую клетку квадрата число 2,3 или 4 так, чтобы сумма чисел в каждой строке и в каждом столбце равнялась 9.
-
Предмет:
Математика -
Автор:
fernm8oj - 6 лет назад
-
Ответов:
0 -
Смотреть
-
- периметр ромба равен 40, а один из углов равен 60°. Найдите площадь ромба, делённую на √3
-
особенность казанского ханства
-
Каковы особенности строения побегов хвойных растений?
-
Предмет:
Биология -
Автор:
jaylynncochran - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
