-
Помогите, пожалуйста,придумать способ доказательства
Тема "Сумма углов треугольника"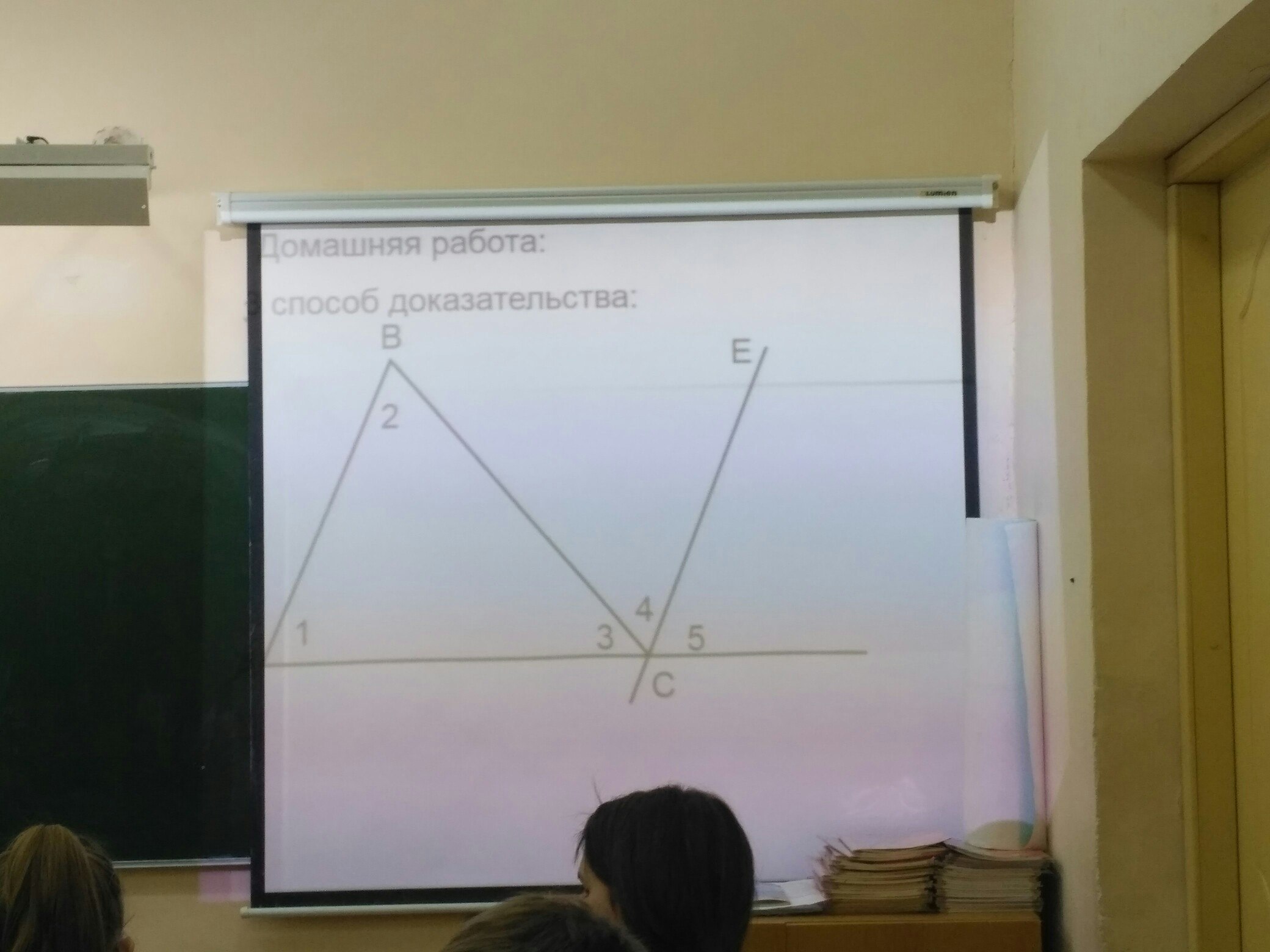
Ответы 1
-
Вероятно, в условии задачи сказано, что АВ║СЕ. Тогда решение такое:∡4+∡5=∡1+∡2, так как углы 4 и 5 составляют внешний угол ΔАВС. ∡1=∡5 как соответственные углы при параллельных прямых и секущей АС. Подставим значение ∡5 в равенство ∡4+∡5=∡1+∡2: ∡4+∡1=∡1+∡2, ∡4+∡1-∡1=∡2⇒∡4=∡2.∡5+∡4+∡3=180°-по свойству развернутого угла, но ∡4=∡2, ∡5=∡1⇒∡1+∡2+∡3=180°, что и требовалось доказать
-
Автор:
lady gaga - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Напишите краткие ответы.
например:
1. Are she sleeping? Yts, she is.
2.Are the birds singing? Yes,..................................
3.Is he reading? Yes,.................................................
4.Is it flying? No,..........................................................
5.Is he running? Yes,.................................................
6.Is she swimming? No,............................................
7.Is thebaby smiling? No,.........................................
8.Is the mam sitting? Yes,........................................
9.Are they dancing? Yes,.........................................
10.Is she watching TV? No,.....................................
11.Is she talking on the telephone? No,................
12.Is he driving a car? No,........................................
13.Are the monkeys eating? No,............................
14.Is he riding a bicycle? No,..................................
15. Are the boys playing football? Yes,...............-
Предмет:
Английский язык -
Автор:
hayden78 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- найдите углы равнобедренного треугольника если разность двух углов 50 градусов
-
какие события происходят на красной площади зимой?
-
Предмет:
Другие предметы -
Автор:
jadonfrench - 6 лет назад
-
Ответов:
4 -
Смотреть
-
- В ходе этой реформы были окончательно отменены рекрутские наборы в армию???
How much to ban the user?
1 hour
1 day
100 years
