ПОМОГИТЕ ПОЖАЛУЙСТА РЕШИТЬ ЗАДАЧУ ПО ГЕОМЕТРИИ 10 КЛАСС.

Через вершину прямого угла С в равнобедренном треугольнике CDE проведена прямая СА перпендикулярная плоскости треугольника. Известно что СА=35 дм, CD=12 корень из 2 дм. Найти расстояние от А до прямой DE.

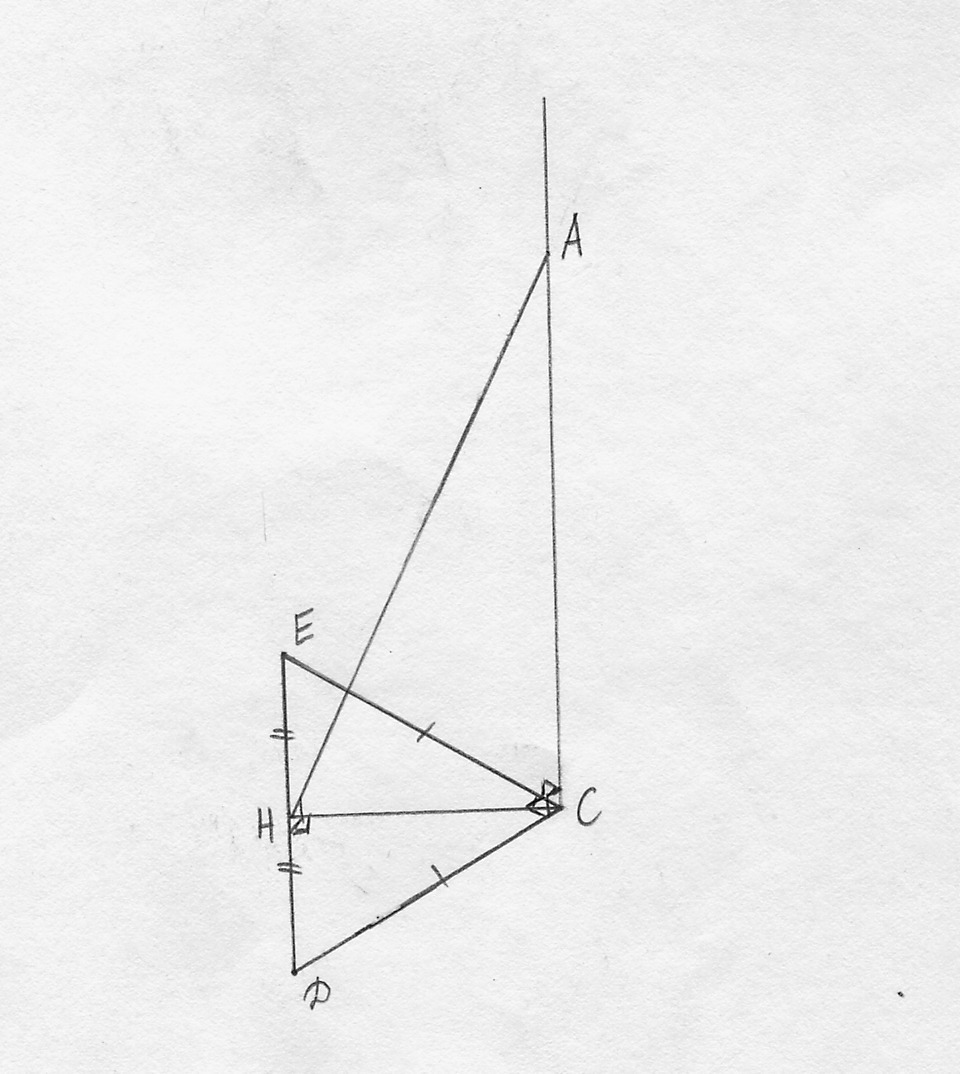
Из т. A опустим перпендикуляр на прямую DE (см. прикрепленный рисунок). Пусть AH - этот перпендикуляр, (длину которого и требуется найти в задаче). Тогда  AH⊥DE. Проведем отрезок  CH в плоскости CDE.Т.к. по условию AC⊥CDE, то AH - наклонная, а AC - перпендикуляр (к плоскости CDE). И AH⊥DE (по построению), тогда по теореме обратной теореме "о трёх перпендикулярах", получаем, что DE⊥CH.Таким образом CH - это высота прямоугольного равнобедренного треугольника CDE. Найдем CH. Для этого найдем DE по т. Пифагора:DE² = CE² + CD² = (12√2)² + (12√2)² = 2*12² + 2*12² = 4*12²,DE = √(4*12²) = 2*12.Т.к. треугольник CDE - равнобедренный, то его высота CH является и медианой. Поэтому DH = EH = DE/2 = 2*12/2 = 12.По т. Пифагора для ΔCDH.CH² = CD² - DH² = (12√2)² - 12² = 2*12² - 12² = 12²,CH = √(12²) = 12.Т.к. AC⊥пл.CDE, то AC⊥CH, и ΔACH прямоугольный, ∠ACH = 90°.По т. Пифагора для ΔACH:AH² = CH² + AC² = 12² + 35² = 144 + 1225 = 1369,AH = √(1369) = 37.Ответ. 37 дм.