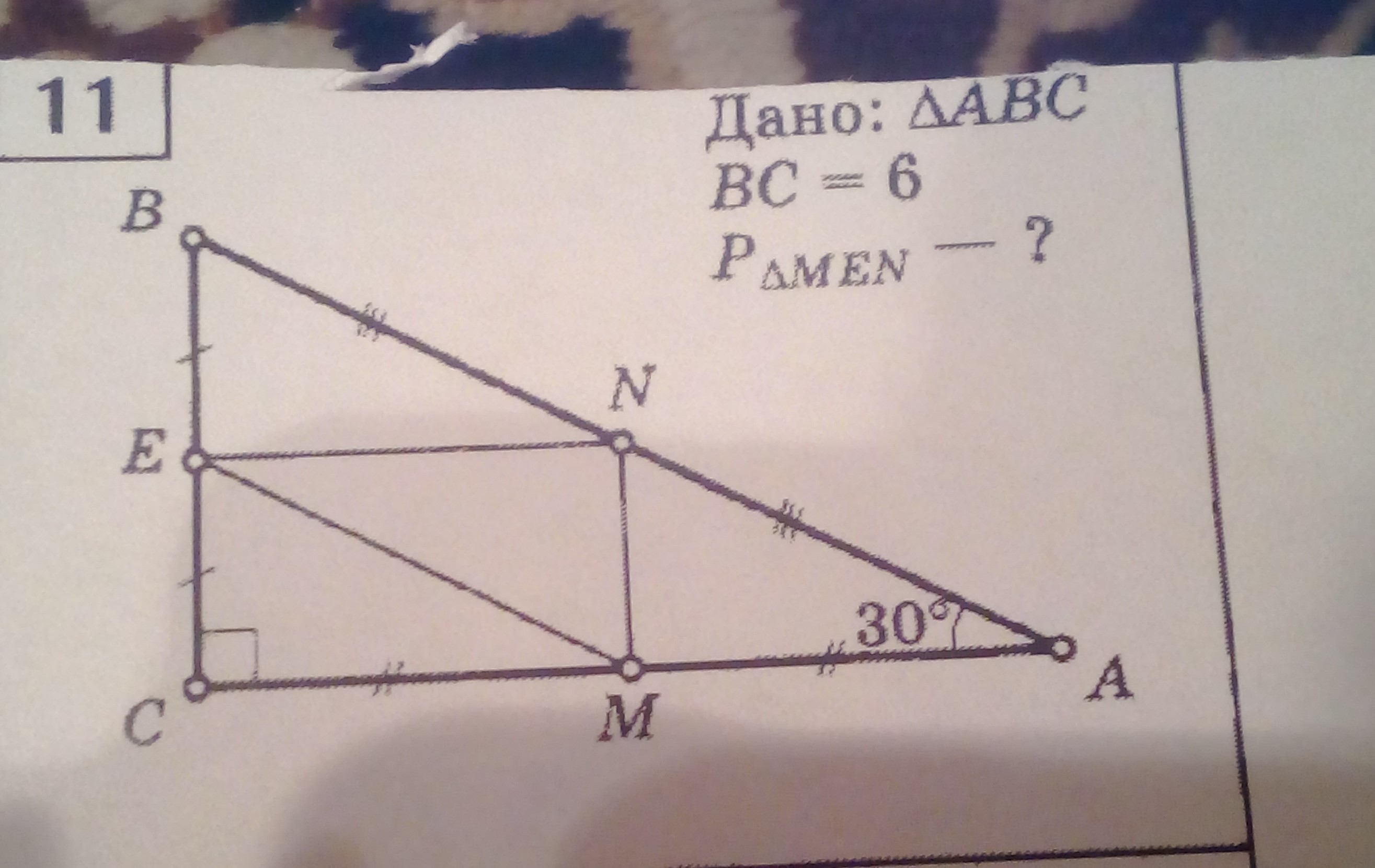
Дано: треугольник ABC , BC=6, Найти:P треугольника men

Спасибо!

пожалуйста

В треугольнике АВС: АВ = 2ВС = 2*6 = 12 (катет, лежащий против угла 30° равен половине гипотенузы)АС = √(12²-6²) = √108 = 6√3Р(АВС) = АВ + ВС +АС = 12 + 6 + 6√3 = 18 + 6√3EN, EM и MN являются средними линиями треугольника АВС по условию, следовательно Р(МEN) = P(ABC)/2 = (18+6√3)/2 = (2(9+3√3))/2 = 9 + 3√3Ответ:  9 + 3√3

Решение:АВ = ВС × 2 = 6 × 2 = 12 (катет лежащий против угла в 30° равен половине гипотинузы) По теореме ПифагораВС² + АС² = АВ²36 + АС² = 144АС² = 144 - 36АС = √108АС = 6√3NM, EM и EN - средние линии => стороны образовавшегося ими треугольника равны половинам сторон данного треугольника (по свойству)Р = 3 + 6 + 3√3 = 9 + 3√3Ответ: Р = 9 + 3√3