-
Известно, что N — серединная точка отрезка KL, а M — серединная точка отрезка KN.
Определи расстояние от точки L до прямой AN.
На плоскости даны точки A,B,C,D,E. Определить какие четыре из них лежат на одной прямой, если BD - расстояние от точки B до прямой AC , а ED - расстояние от точки E до прямой BD.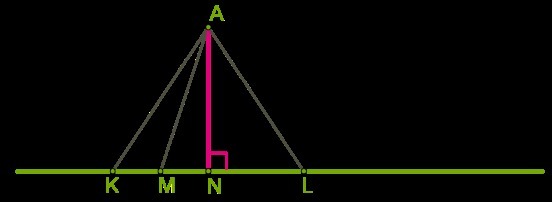
-
Предмет:
Геометрия -
Автор:
nonagentry - 5 лет назад
-
Ответы 1
-
Обе задачи на тему «Теорема о единственности опущенного перпендикуляра»
1) Расстояние от точки до прямой измеряется длиной проведенного между ними перпендикуляра. На рисунке приложения отрезок АN перпендикулярен отрезку KL. Отрезок LN- перпендикуляр между точкой L и прямой АN и является расстоянием от точки L до прямой AN. Если КL=28, то LN=KL:2=28:2=14 см
2) Расстояние от точки до прямой измеряется длиной проведенного между ними перпендикуляра., поэтому точка В не лежит на прямой АС, а т. D лежит, и отрезок ВD перпендикулярен прямой АС. Т.к. ЕD – расстояние от точки Е до прямой ВD, то ЕD перпендикулярна прямой ВD. Из данной точки (Е), не лежащей на данной прямой (BD), можно опустить на эту прямую перпендикуляр, и при том только один (теорема). Поскольку прямые АС⊥BD , а ЕD перпендикулярна BD, а т.D принадлежит АС, то точка Е также лежит на прямой АС. Следовательно, на прямой лежат точки А, D, Е и С. (При этом точка Е может располагаться на прямой как по одну, так и по другую сторону от точки D)

-
Автор:
foxy100 - 5 лет назад
-
0
-
-
Добавить свой ответ
-
Решите уравнение:
1) -х = -0,7
2) -х = 1
3) -х - 1 = -2,5
4) х+3 = -1
5) -х = -8,1 + 9,1
6) х - 2 1/7 = -3 1/7
7) х + 4,8 = -2,2
8) 5,4 - х = 7
9) -х + 1 = -4 1/3-
Предмет:
Математика -
Автор:
corbin - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
решите задачу по алгебре с помощью уравнения .8 класс .
-
Предмет:
Алгебра -
Автор:
daniellalambert - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Классификация потребностей человека. Помогите пожалуйста.
-
Предмет:
Обществознание -
Автор:
jasmine - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Деление с остатком: 12:3, 17:3,11:4,24:6
-
Предмет:
Математика -
Автор:
zoey82 - 5 лет назад
-
Ответов:
5 -
Смотреть
-
