Через точку А на поверхности шара проведена секущая плоскость. Площадь полученного сечения равна 21. Если угол между плоскостью и радиусом шара, проведённым в точку А, равен 60 градусов, то площадь поверхности шара равна...
Решите пж срочно, даю 25 баллов
(P.S. если можно, то с рисунком)

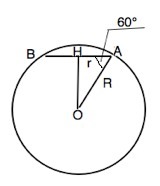
В приложении дан схематический риунок сечения через  диаметр секущей плоскости и центр шара. 

Сечение шара всегда круг. 

Диаметр сечения АВ, радиус АН. 

АО=R

Площадь круга по условию 21. 

S= \pi r^2=21⇒

r=AH= \sqrt{ \frac{21}{ \pi } }

 R= \frac{AH}{cos60^o} = \sqrt{ \frac{21}{ \pi } } : \frac{1}{2} = \frac{2* \sqrt{21} }{ \sqrt{ \pi }}

S(шара)= \frac{4 \pi R^2}{3}= 4* \pi *4*( \frac{ \sqrt{21} }{ \sqrt{ \pi }} )^2 :3=112(ед. площади)