Задать вопрос Регистрация
Помочь другим

  • Диагонали трапеции

    ABCD с основаниями

    AB и

    CD
    пересекаются в точке

    O.
    Найти

    AB если известно, что

    OB=18,

    BD=66,

    DC=72.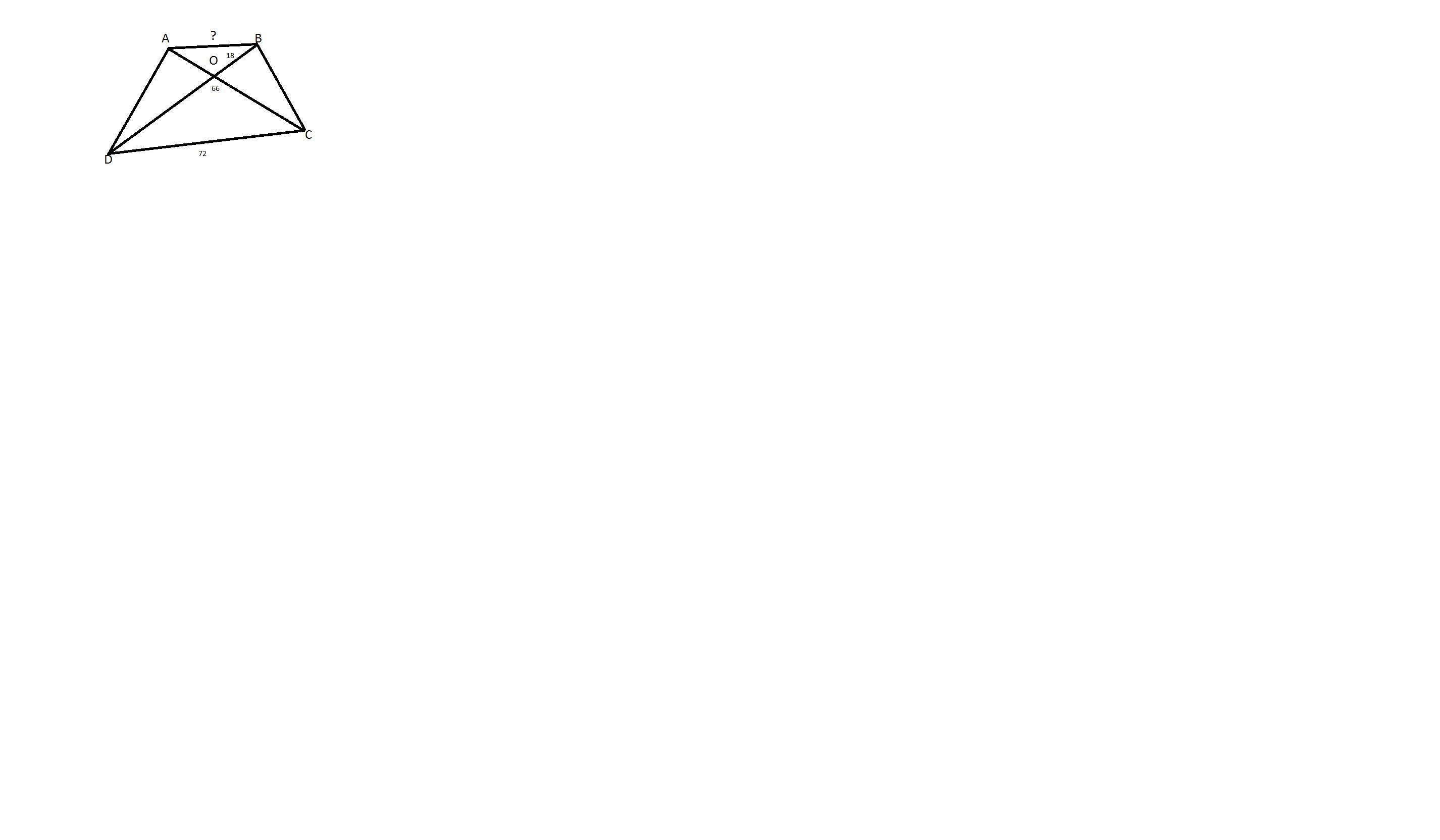

    question img

Ответы 1

  • накрест лежащие углы равны: ∠ОАВ=∠ОСD, ∠ОВА=∠ОDC)ΔАОВ и ΔСОD подобны (по двум углам), из подобия следует \frac{AB}{DC} = \frac{OB}{OD} \\ AB= \frac{OB*DC}{OD}, (OD=BD-OB) \\ AB= \frac{OB*DC}{BD-OB} \\ AB= \frac{18*72}{66-18} = \frac{6*3*8*9}{48} =3*9=27 Ответ: АВ=27 единиц

    • Автор:

      rosie62
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years