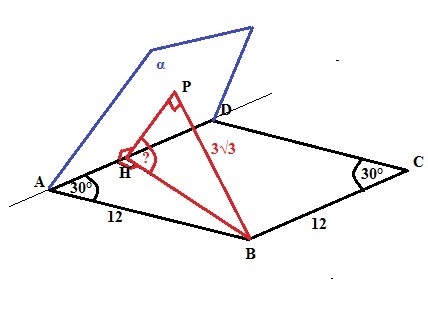
Через сторону AD ромба ABCD проведена плоскость альфа, удаленная от BC на расстояние равное 3 корней из 3 см. Найдите угол между плоскостью ромба и плоскостью альфа.

Угол между двумя пересекающимися плоскостями (двугранный угол) измеряется градусной мерой линейного угла между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения.Опустим на плоскость α перпендикуляр ВР (это и есть расстояние от стороны ВС до плоскости α, так как ВС параллельна AD - линии пересечения плоскостей α и АВСD)   и проведем через этот перпендикуляр плоскость, перпендикулярную ребру двугранного угла между плоскостями (стороне АD - линии пересечения плоскостей АВСD и α).Тогда искомый угол между плоскостями - это угол ВНР между высотой ромба ВН и отрезком НР, где точка Р - основание перпендикуляра ВР на плоскость. В прямоугольном треугольнике АВН против угла <A=30° (противоположные углы ромба равны) лежит катет ВН, равный половине гипотенузы - стороны ромба АВ. То есть ВН= 6.В прямоугольном треугольнике ВРН синус угла <Н=ВР/ВН (отношению противолежащего катета к гипотенузе).Sin(BHP)=3√3/6 = √3/2. Значит искомый угол между плоскостями равен arcsin(√3/2) = 60°.Ответ: 60°.