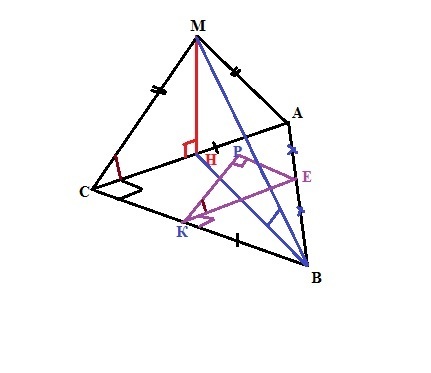
Треугольник ACB - прямоугольный(C=90 градусов), AC=CB=3 см. Треугольник AMC имеет общую сторону AC с треугольником ACB, AM=CM=корень из 6. Плоскости треугольников взаимно перпендикулярны

1. По теореме о трех перпендикулярах наклонная МС перпендикулярна прямой ВС, так как ее проекция НС перпендикулярна прямой ВС, что и требовалось доказать.2. Углом между плоскостью (АВС) и не перпендикулярной ей прямой (МВ) называется угол между этой прямой и ее проекцией на данную плоскость - угол МВН.МН - высота равнобедренного треугольника АМС, проведенная к основанию АС и делит его пополам (свойство). Следовательно, СН=3/2см. Тогда в прямоугольном треугольнике МСН: МН=√6-9/4)=√15/2см.А в треугольнике НСВ гипотенуза ВН=√(9/4+9)=3√5/2см.В прямоугольном треугольнике МНВ:Tg(MBH)=MH/BH = √3/3. (отношение противолежащего катета к прилежащему). Значит искомый угол равен  α=arctg(√3/3) = 30°.3. Расстояние от точки Е до плоскости МВС, не содержащей эту точку, есть длина отрезка ЕР перпендикуляра, опущенного из этой точки на данную плоскость.В прямоугольном треугольнике ЕРК: ЕК=3/2см (так как ЕК - средняя линия треугольника АВС). <PKE=<MCA как углы с параллельными сторонами (плоскость МСА параллельна плоскости РКЕ).Sin(<MCA)=MH/MC = (√15/2)/√6=√3*√5/(2√3*√2) = √10/4.Тогда РЕ= ЕК*Sin(<PKE) = (3/2)*(√10/4) = 3√10/8 ≈1,186см. Ответ: расстояние от точки Е до плоскости ВМС равно 3√10/8 ≈1,186см.