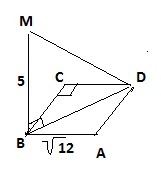
10. АВСД – квадрат, BM перпендикулярна ABC. Найдите отрезок ДМ, если АВ = √(12) см. а ВМ = 5 cм.
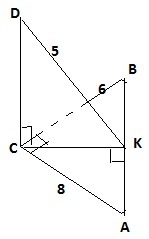
11. Треугольник АВС прямоугольный, С = 90°, АС = 8 см, ВС = 6 см. Отрезок СД перпендикуляр к плоскости AВС. Найдите СД, если расстояние от точки Д до стороны AВ равно 5 см.

10. Сторона квадрата равна √12, тогда диагональ квадрата по теореме Пифагора ВD=√(2*√12)²=√24=2√6смМD=√(MB²+BD²)=√(25+24)=√49=7cм.11. Из прямоугольного ΔАВС по т. Пифагора АВ=√(СВ²+СА²)=√(36+64)=10см. Перпендикуляр, опущенный из вершины прямого угла на гипотенузу делит треугольник на подобные треугольники, поэтому АВ/АС=АС/АК    АК=АС²/АВ=64/10=6,4см. Используем теорему о трех перпендикулярах⇒ DC⊥ABC, DK⊥АВ, CK⊥AB, находим СК=√(АС²-АК²)=√(64-40,96)=√23,04=4,8. DC⊥CK⇒DC=√(DK²-CK²)=√(25-23,04)=√1.96=1,4cм..К решению прикреплены 2 файла..