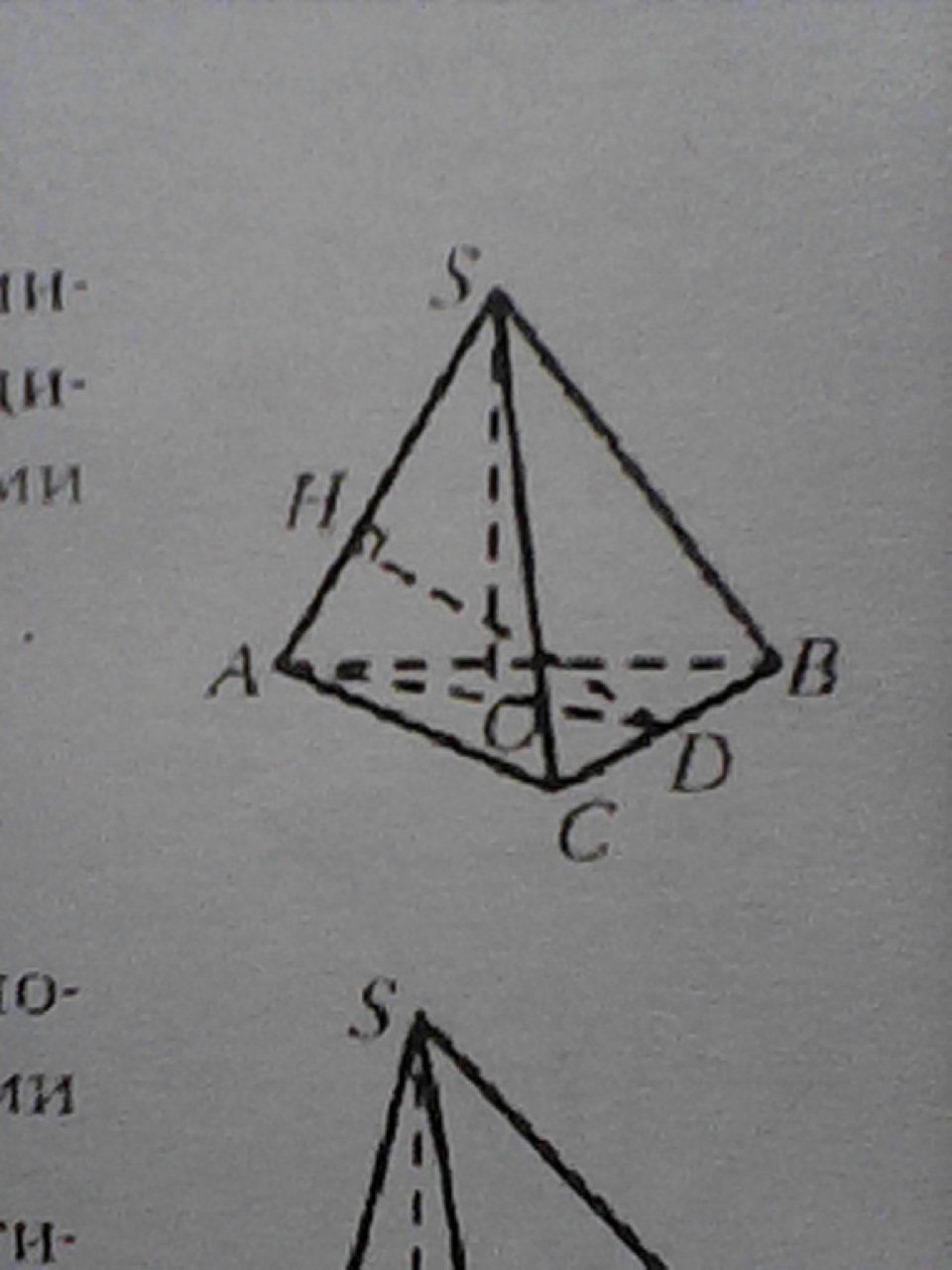
Боковое ребро правильной треугольной пирамиды равно 25, а высота пирамиды равна 24. Найдите расстояние между скрещивающимися ребрами пирамиды.

Расстояние между скрещивающимися прямыми - это их общий перпендикуляр.Построить плоскость  ASD. Прямая AS лежит в этой плоскости. Прямая CB пересекает эту плоскость в точке D ⇒ прямые AS и CB скрещивающиеся  ⇒  нужно найти расстояние между прямыми AS и CB.В ΔABC  AD - высота ⇒  BC⊥AD  ⇒  BC ⊥ (ASD)  ⇒ BC⊥DHТак как DH⊥AS и DH⊥BC  ⇒DH - расстояние между прямыми AS и CBВысота правильной треугольной пирамиды опускается в центр вписанной и описанной окружности равностороннего треугольника основания.  ⇒ R=AO  радиус описанной окружностиr = OD радиус вписанной окружностиВ равностороннем треугольнике R = 2r  ⇒  AO = 2 ODΔASO прямоугольный, ∠AOS=90°. Теорема ПифагораAO² = AS² - SO² = 25² - 24² = (25-24)(25+24)=49AO = √49 = 7sin∠A = SO/AS = 24/25 = 0,96OD = 1/2 AO = 7/2 = 3,5AD = AO + OD = 7 + 3,5 = 10,5ΔAHD - прямоугольный, ∠AHD=90°HD = AD*sin∠A = 10,5 * 0,96 = 10,08Ответ: расстояние между скрещивающимися ребрами пирамиды 10,08