-
Докажите, что если на рисунке угол B и угол D прямые и AD=BC, то треугольники ABC=CDA. Можно объяснение развернутое.
-
Предмет:
Геометрия -
Автор:
slickbraun - 6 лет назад
-
Ответы 1
-
Отложим на продолжении DС в сторону от D отрезок DC1, равный АB. Соединим C1 и А.
В ∆ АDC1 угол АDC=90° (смежный углу АDС). В ∆ АDC1 и ∆ АBС катет DС1=АВ по построению, АD =СВ по условию. ⇒
∆ АDC1=∆ АBС по первому признаку равенства треугольников. .
Значит, АC1=АС, поэтому ∆ АC1С - равнобедренный, АD - его высота и медиана, ⇒ ∆ АDC1=∆ АDС.
Так как ∆ АBС=∆ АDC1( доказано), то ∆ АВС=∆ АDС, ч.т.д.
-------------
Если без подробного доказательства, то по признаку равенства прямоугольных треугольников:
Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.⇒
∆ ABC=∆ CDA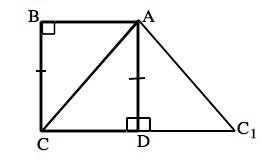
-
Автор:
davispgub - 2 года назад
-
6
-
-
Добавить свой ответ
-
Вот тебе лёгкий вопрос. Выбери из списка программы для компьютера. 1. Блокнот 2. Монитор 3. Калькулятор 4. Мышь
-
Предмет:
Информатика -
Автор:
guillermoajep - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
какое значение имеет почта для человека или общества( до 5 предложений)
-
Предмет:
Окружающий мир -
Автор:
zaidenfroh - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Складзіце з гукаў словы
1. А, ц, й, к, ы, а, а
2. З', ц', э, у, сі, л'
3й, н', й, э, а, а, ч-
Предмет:
Беларуская мова -
Автор:
savannall8h - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
преобразовать произведение в многочлен
(x+y)(z+1)=
(x+2)(y-z)=
(x-1)(x+y-3)=
(x-y)(x+y)=
(x+1)(x+1)=
