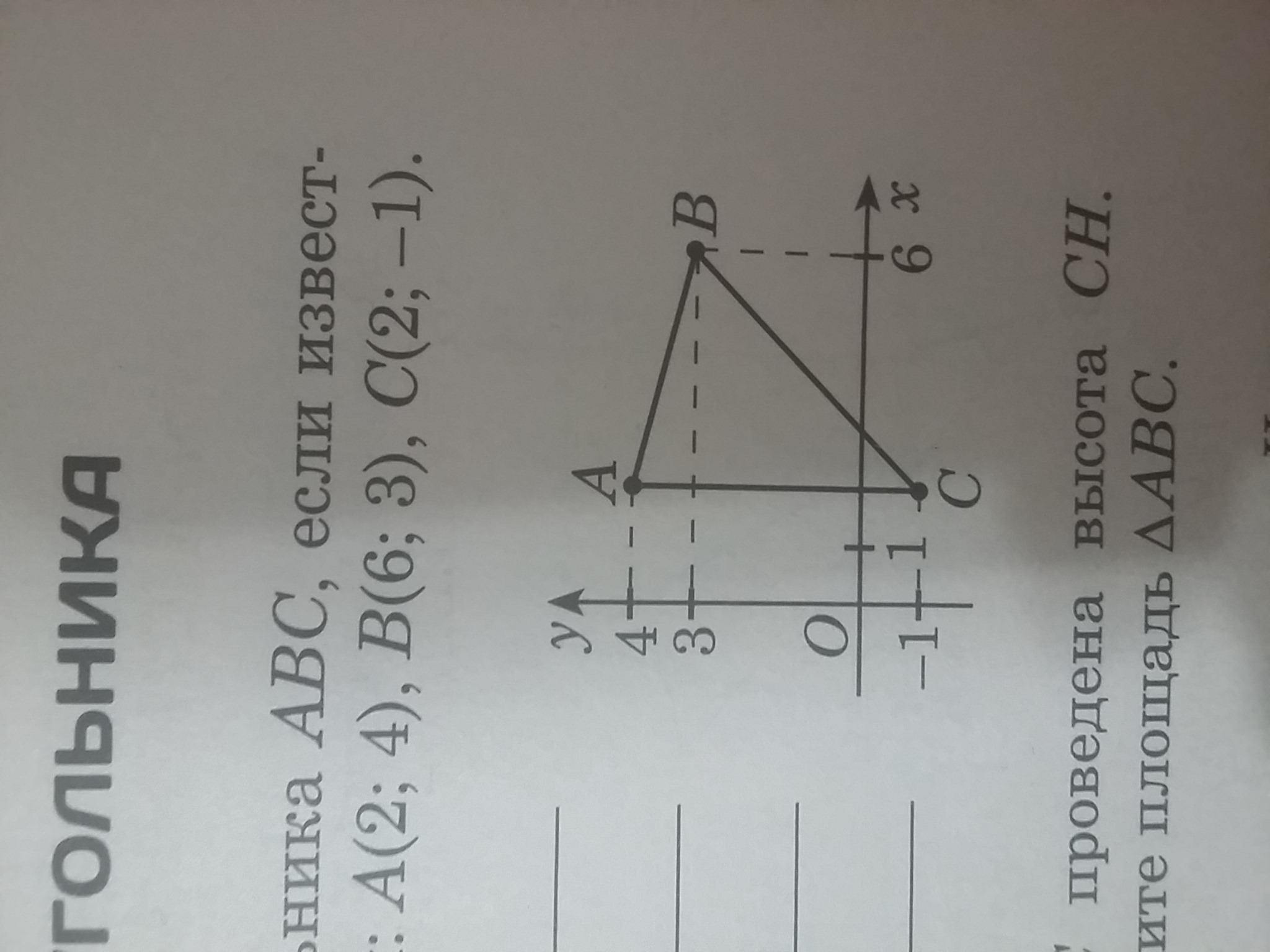
Найдите площадь треугольника ABC, если известеы координаты его вершин: А(2;4),В(6;3),С(2;-1)

Ответ: =10

Объяснение:

Найдем длины АВ, ВС и АС.

АВ=\sqrt{Xa-Xb)^2 +(Ya-Yb)^2} = \sqrt{(6-2)^2+ (3-4)^2} =\sqrt{17}

BC=\sqrt{Xc-Xb)^2 +(Yc-Yb)^2} = \sqrt{(2-6)^2+ (-1-3)^2} =\sqrt{32}

AC=\sqrt{Xa-Xc)^2 +(Ya-Yc)^2} = \sqrt{(2-2)^2+ (4-(-1))^2} =\sqrt{25} =5

Длины сторон - иррациональные числа =>  теорему Герона применять неудобно.

Найдем cos∡B по теореме косинусов

AC²=AB²+BC²-2AB*BC*cos∡B

25=17+32-2*√17*√32*cos∡B

2*√17*√32*cos∡B =24

√17*√32*cos∡B =12

cos∡B = 3/√34

sin∡C=\sqrt{1-cos^2 C} = \sqrt{1-9/34}= 5/\sqrt{34}

S(ABC)= AB*BC*sin∡C /2=5 \sqrt{32*17*/34}/2 =5*4/2=10