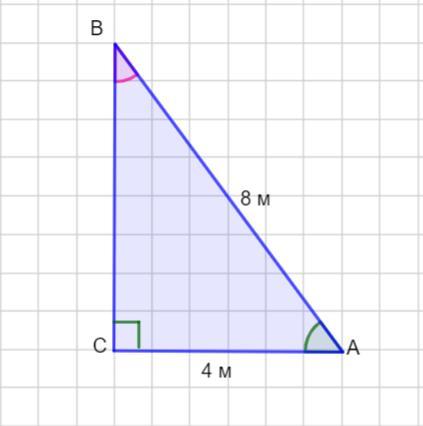
у прямокутному трикутнику ABC гіпотенуза AB дорівнює 8м, а катет AC - 4м. Знайдіть другий катет І гострі кути трикутника

Ответ:

ВС =4√3 м, ∠ В =30°, ∠А =60°.

Объяснение:

В прямоугольном треугольнике АВС гипотенуза АВ равна 8 м, а катет АС равен 4 м. Найти другой катет и острые углы треугольника.

Пусть дан Δ АВС - прямоугольный, ∠С =90°

АВ = 8м - гипотенуза, АС =4 м - катет. Найдем катет ВС, используя теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

AB^{2} =AC^{2} +BC^{2} ;\\BC^{2} =AB^{2}-AC^{2};\\BC =\sqrt{AB^{2}-AC^{2}};\\BC =\sqrt{8^{2} -4^{2} } =\sqrt{(8-4)(8+4)} =\sqrt{4\cdot12} =\sqrt{4\cdot4\cdot3} =4\sqrt{3}  

Катет ВС =4√3 м.

В ΔАВС катет АС =4 м, гипотенуза АВ =8 м. Катет АС в 2 раза меньше гипотенузы. Значит, этот катет лежит напротив угла в 30°.

Тогда ∠ В =30°.

Сумма острых углов прямоугольного треугольника равна 90°.

∠А =90°-∠В;

∠А =90 °-30°=60°

Значит, острые угла прямоугольного треугольника равны 30° и 60°.

#SPJ5