Задать вопрос Регистрация
Помочь другим

  • Найдите косинус угла между векторами   a=n+2m и b=3n-m, если m⊥n, |m|=|n|=1.

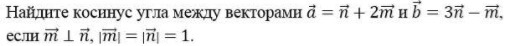
    question img

Ответы 1

  • \vec n⊥\vec m;  |\vec n|=|\vec m|=1\vec a = \vec n + 2\vec m; \vec b = 3\vec n - \vec mЕдиничные векторы  \vec n⊥\vec m можно рассматривать как ортонормированный базис плоскости. Тогда в этой системе координаты векторов \vec a (1; 2) и \vec b (3; -1)Длины векторов|\vec a|= \sqrt{1^2+2^2} = \sqrt{5} \\ \\ |\vec b|= \sqrt{3^2 +(-1)^2} = \sqrt{10} Скалярное произведение векторов\vec a * \vec b = |\vec a| * |\vec b|*cos(\vec a, \vec b) \\ \\ cos (\vec a, \vec b)= \frac{\vec a * \vec b}{|\vec a| * |\vec b|} = \frac{1*3 + 2*(-1)}{ \sqrt{5}* \sqrt{10} } = \frac{1}{5 \sqrt{2} } cos∠(\vec a, \vec b) = 1/(5√2) ≈ 0,1414
    answer img

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years