-
помогите пожалуйста с геометрией срочно!МНОГО БАЛОВ
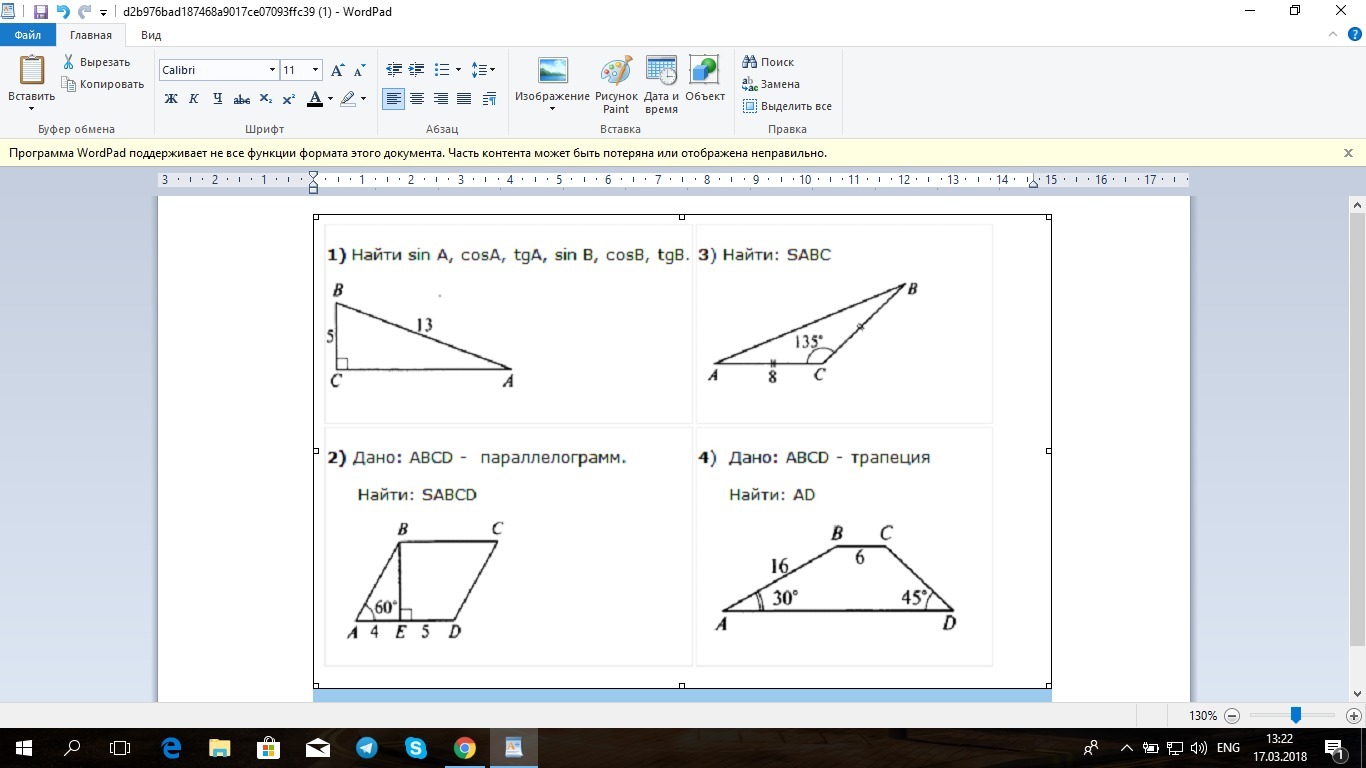
-
Предмет:
Геометрия -
Автор:
lassiemoex - 6 лет назад
-
Ответы 1
-
Задача 1:1)Рассмотрим прямоугольный треугольник ABC:Используя т. Пифагора, найдем катет СА169 = 25 + CA^2CA^2 = 144CA = 122) sin - отношение противолежащего катета к гипотенузеcos - отношение прилежащего катета к гипотенузе tg - отношение противолежащего катета, к прилежащемуТ.о tgA = 5/12sinA = 5/13cosA = 12/13tgB = 12/5cosB = 5/13sinB = 12/13Задание 2:1) Рассмотрим прямоугольный треугольник ABE: Так как угол BAE = 60, то угол ABE = 30Против угла в 30 лежит катет равный половине гипотенузы:AB = 4×2 = 8Т. Пифагора:64 =16 + BE^2BE^2 = 48BE = 4 корня из 3Площадь парал- ма равна произведению основания на высоту, значит, S = (4 + 5)× 4 корня из 3 = 36 корней из 3Задание 3:Так как треугольник равнобедренный, то AC = CB = 8Т.о S = 1/2 × AC × CB × sin135 = 1/2×64× корень из 2 / 2 = 16 корней из 2Задание 4:Рассмотрим трапецию ABCD:Опустим высоты BH и CMРассмотрим прямоугольный треугольник ABH:Против угла в 30 лежит катет равный половине гипотенузы, значит, BH = 16/2 = 8Т. Пифагора:256 = 64 + AH^2AH^2 = 192 AH = 8 корней из 3Так как BCMH - прямоугольник, то противоположные стороны равны:BH = СM = 8BC = HM = 6Рассмотрим прямоугольный треугольник CDM:Так как треугольник равнобедренный, то CM = MD = 8AD = 8 корней из 3 + 6 + 8 = 8 корней из 3 + 14
-
Автор:
maria43 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Запишите 3 числа, которые больше 1,34, но меньше 1,36
-
Предмет:
Математика -
Автор:
belch8li6 - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Склонить слова: репа, окно, тишь
-
Предмет:
Русский язык -
Автор:
cristóbalzclw - 6 лет назад
-
Ответов:
10 -
Смотреть
-
-
помогите пж срочно
Запеши и отгадай загадки раскрывая скобки. в первой загадке используй глаголы
в форме 3 го лица мн ч и 1 лиц ед ч укажи грамматичиские признаки которые помогли тебе правильно написать окончяния глаголов 1 меня (бить) (колотить) (ворочать) (резать) я всё (терпеть) и всем добром (платить) 2 (дышать растёт а ходить не (мочь) 3 (сидеть) зеленеть летит (желтеть) (упасть) (почернеть)-
Предмет:
Русский язык -
Автор:
mercedesmeyers - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Как обозначается глина,пригодный газ,каменная соль на картах
-
Предмет:
Окружающий мир -
Автор:
anayasaunders - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
