Катеты прямоугольного треугольника равны 5 см и 6 см. Найдите площадь проекции этого треугольника на плоскость, если плоскость треугольника наклонена к плоскости проекции под углом 60°.

Ответ:

Площадь проекции этого треугольника на плоскость равна 7,5 см².

Объяснение:

Катеты прямоугольного треугольника равны 5 см и 6 см. Найдите площадь проекции этого треугольника на плоскость, если плоскость треугольника наклонена к плоскости проекции под углом 60°.

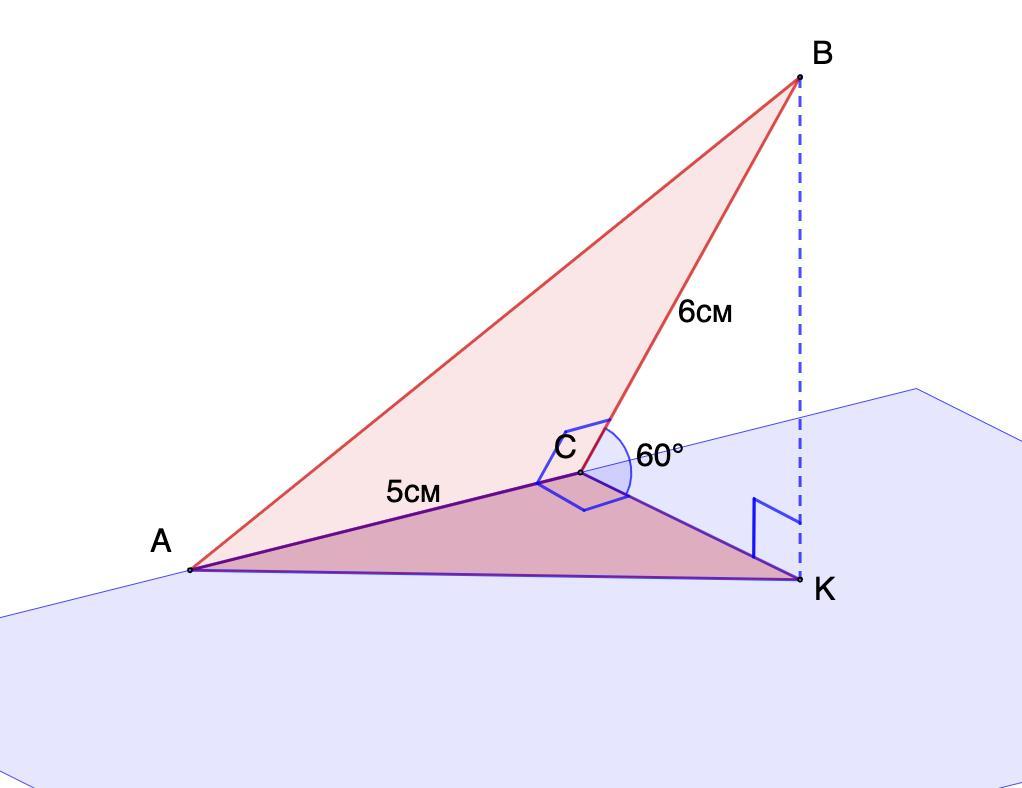
Дано: ΔАВС - прямоугольный;

АС = 5 см; ВС = 6 см - катеты;

ΔАСК - проекция АВС на плоскость.

Угол между ΔАВС и ΔАСК равен 60°.

Найти: S(ACK)

Решение:

• Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей.

ВС ⊥ АС

СК - проекция ВС на плоскость.

• Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.

⇒ КС ⊥ АС.

⇒ ∠ВСК - угол между ΔАВС и ΔАСК.

∠ВСК = 60°.

Рассмотрим ΔСВК - прямоугольный.

∠ВСК = 60°

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠СВК = 90° - 60° = 30°

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ СК = СВ : 2 = 6 : 2 = 3 (см)

Рассмотрим ΔАСК - прямоугольный.

• Площадь прямоугольного треугольника равна половине произведения его катетов.

⇒ \displaystyle S(ACK)=\frac{1}{2}\cdot AC \cdot CK = \frac{1}{2}\cdot 5 \cdot 3=7,5  (см²)

Площадь проекции этого треугольника на плоскость равна 7,5 см².

#SPJ1