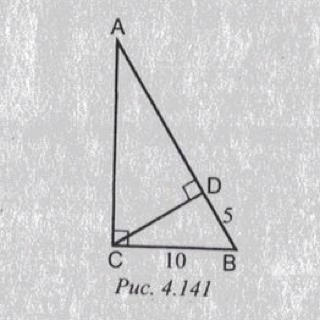
Рис. 4.141. Найти АD.

В прямоугольном треугольнике АВС угол С=90°. СD  - высота. ВС=10, ВD=5.Найти АD. ––––––––––––––––––––––––––Решение задачи имеет несколько вариантов.  1) В прямоугольном ∆ ВСD катет ВD равен половине гипотенузы ВС. ⇒ВD противолежит углу 30° ( свойство). Тогда угол CBD=90°-30°=60°, а угол САВ=30°АВ=2СВ=20АD=AB-BD=20-5=15 (ед. длины)2)Катет есть среднее пропорциональное между гипотенузой треугольника и проекцией катета на неё.⇒ВС²=АВ•BD100=(5+AD)•5100=25+5AD 5AD=75AD=75:5=15 (ед. длины)3) Из ∆ ВСD по т.Пифагора СD²=CB²-BD²=100-25=75В прямоугольном треугольнике высота, проведенная к гипотенузе - среднее пропорциональное между отрезками, на которые она , делит гипотенузу. СD²=AD•BD75=AD•5⇒AD=15----------------- 4)Высота из прямого угла делит исходный треугольник на подобные. ⇒∠СAD=∠BC sinBCD=BD/CB=1/2⇒sin CAB=1/2⇒AB=CB/sinCAB=10/0,5=20AD=AB-BD=20-5=15 ед. длины