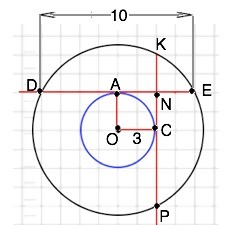
Две окружности имеют общий центр О. К меньшей из них провели перпендикулярные касательные DE и KP, пересекающиеся в точке N. Найдите DN, если DE=10 сама радиус меньшей окружности равен 3 см

Отрезки касательных, проведенных к окружности из одной точки, равны. 

NA=NC. 

Радиусы, проведенные в точку касания, перпендикулярны касательной. 

∠ОАN=∠OCN=90° 

Угол ANC=90° по условию. AN║OC;  NC║OA; 

ОА=ОС – радиусы => OANC- квадрат.  AN=OC=3 см

В большей окружности DE- хорда, отрезок ОА - перпендикулярен ей. Перпендикуляр, проведенный из центра окружности к хорде, делит ее пополам. 

AD=AE=5 см

DN=DA+AN=5+3=8 см