-
на рисунке 129 две окружности имеют общий центр О. К меньшей из них провели перпендикулярные касательные АВ и CD , пересекающиеся в точке К. Найдите радиус меньшей окружности , если АК=2см, ВК=6см
пожалуйста , напишите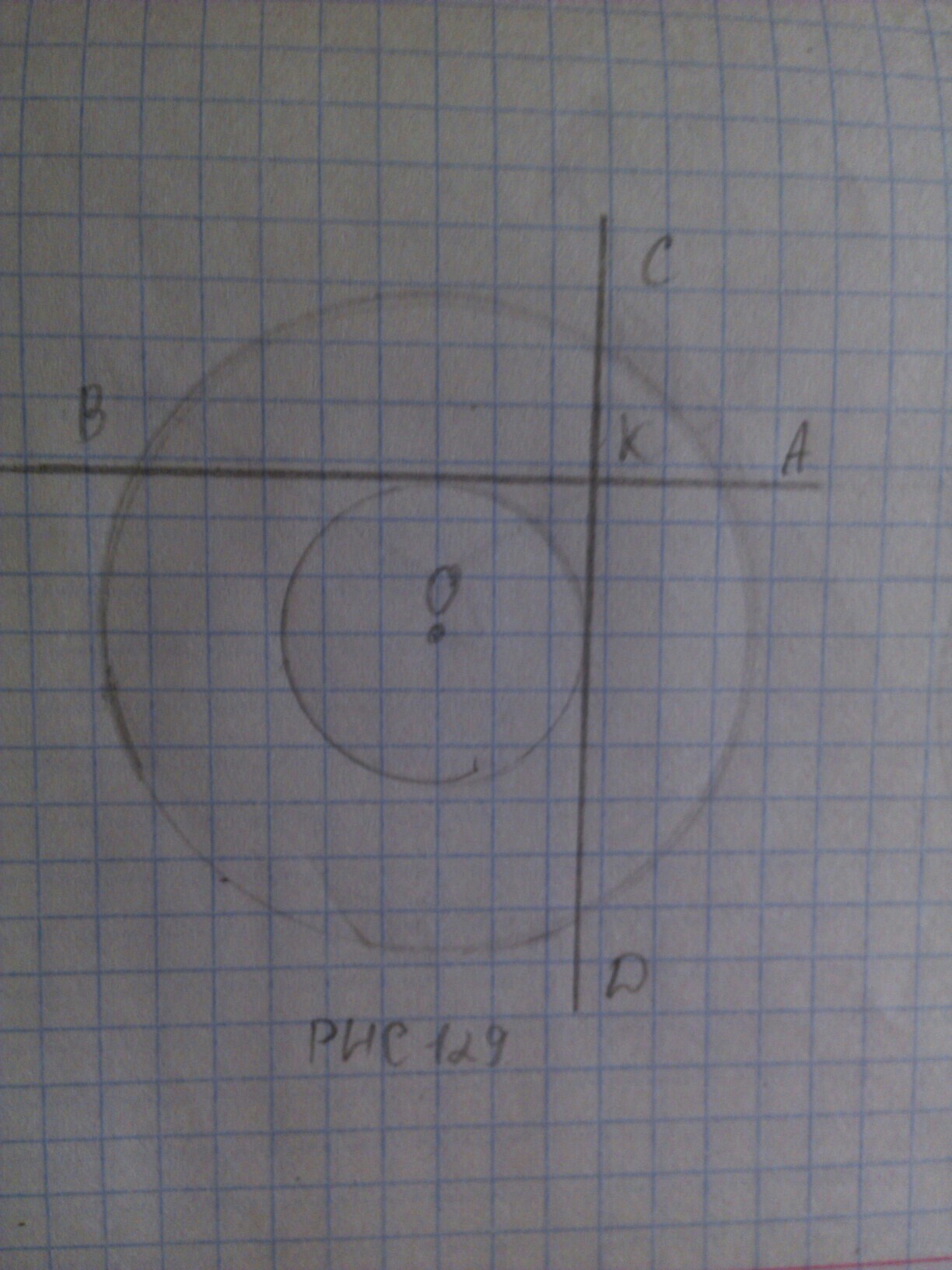
Ответы 1
-
Подробно:Обозначим М точку касания меньшей окружности с АВ, Е – точку касания с СD. (см. рисунок приложения)
Радиус, проведенный в точку касания, перпендикулярен касательной.
Отрезки касательных, проведенных к окружности из одной точки, равны.
КМ=КЕ,- отрезки касательных, МО=ОЕ – радиусы.
В четырехугольнике ОМКЕ углы прямые, противоположные стороны параллельны и равны.
ОМКЕ - квадрат.
АВ - хорда большей окружности. Перпендикуляр, проведенный к хорде из центра, делит ее пополам. =>
АМ=ВМ=(2+6):2=4
МА=4, АК=2 => МК=2 см
МК=ОЕ=радиус меньшей окружности.
r=2 см.

-
Автор:
sparks - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Слова с парной согласной п,ф,к
-
Предмет:
Русский язык -
Автор:
carr - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Program summa;
Uses Crt;
Var S,a,n,i:integer;
Begin
Write('vvod kol-va chisel=');
Readln(n);
If n<=100 then
Write('vvod chisel=');
S:=0;
for i:=1 to n do begin
read(a);
If ((a mod 3)=0) and ((a mod 10)=2) then
S:=S+a;
End;
Writeln('vivod summi=',S);
readkey;
End.
что не так в этой программе? исправьте пж-
Предмет:
Информатика -
Автор:
flopsyhardy - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
выпиши виды животных занесенных в Красную книгу Украины:
Устрицы, мидии, рапаны, осетр, севрюга, бычки, кефаль, дельфин-белобочка, скумбрия, дельфин-афалина, катран.-
Предмет:
Биология -
Автор:
jimmuyolsen - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
ЛЮДИ!!
Нужно СРОЧНО решить эту страницу!
ВСЮ с 1-12 номера!!!
ФОТО:-
Предмет:
Математика -
Автор:
alannazmub - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
