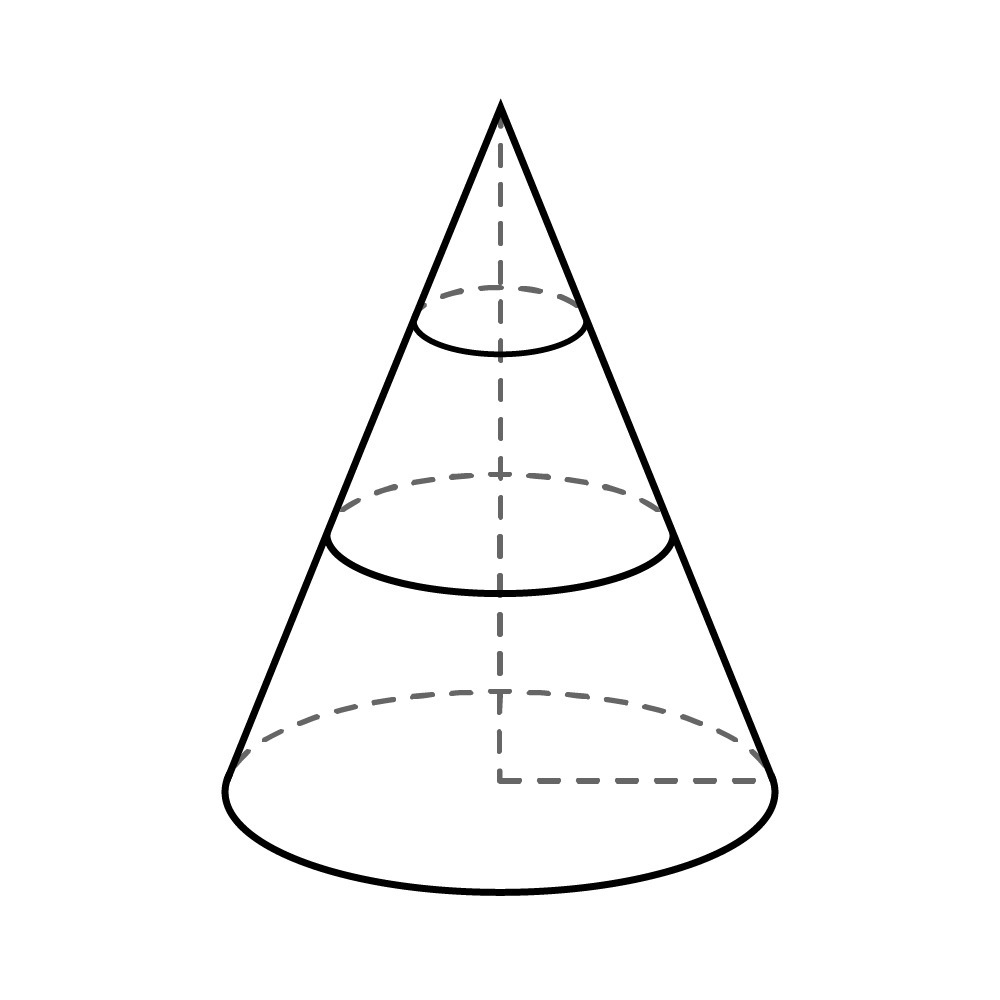
Две плоскости, параллельные основанию конуса, делят его высоту на три равные части. Объём средней части конуса равен 14. Найдите объём всего конуса.

Пусть V₁ - объём верхнего конуса с высотой MN;V₂ - объём конуса с высотой MK;V₃ - объём конуса с высотой MP  - этот объём нужно найтиV₂ - V₁ = 14По условию высота конуса MP разделена на три равных частиh = MN = NK = KPΔMKB ~ ΔMNA  подобны по двум углам: прямому и общему остромуОбъёмы подобных фигур относятся как коэффициент подобия в кубеV₂ = 8V₁По условию  V₂ - V₁ = 148V₁ - V₁ = 14    ⇒   7V₁ = 14   ⇒    V₁ = 2ΔMPC ~ ΔMNA  -  подобны по двум углам: прямому и общему остромуV₃ = 27V₁ = 27 * 2 = 54Ответ: объём всего конуса равен 54