-
Помогите с 58 во вложении
Не могу понять как делать.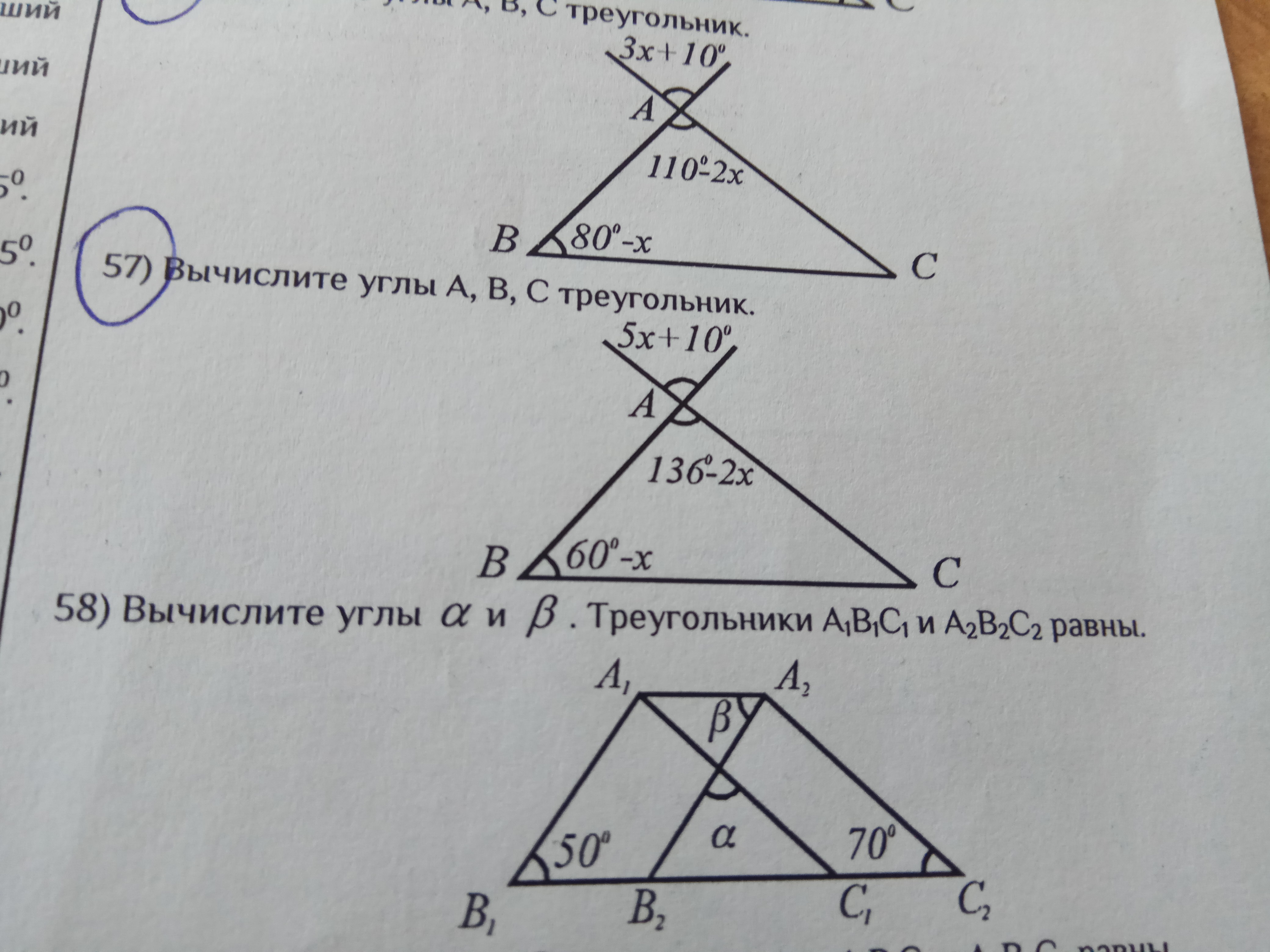
-
Предмет:
Геометрия -
Автор:
hot saucerzyo - 6 лет назад
-
Ответы 2
-
В равных треугольниках против равных сторон лежат равные углы. А1В1=А2В2, В1С1=В2С2 и А1С1=А2С2.Тогда <A2B2C2=<F1B1C1=50°, а <A1C1B1=<A2C2B2=70°.<B1A1C1=<B2A2C2=180°-50°-70°=60°(по сумме углов треугольника).Сумма углов треугольника равна 180°, значит α = 180°-<A2B2C2-<A1C1B1 = 180°-50°-70°=60°.<α=<B1A1C1=60°, а это соответственные углы при прямых А1В1 и А2В2. Значит прямые А1В1 А2В2 параллельны. Но они и равны, как соответственные стороны равных треугольников А1В1С1 и А2СВ2С2.Следовательно, А1В1В2А2 - параллелограм по третьему признаку: "Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм" и угол β=50°, как противоположный угол параллелограмма.Ответ: α=60°, β=50°.

-
Автор:
einsteinthornton - 6 лет назад
-
0
-
-
∠А₂В₂С₂ = ∠А₁В₁С₁ = 50°∠А₁С₁В₁ = ∠А₂С₂В₂ = 70°α = 180 - ∠А₂В₂С₂ - ∠А₁С₁В₁ = 180 - 50 - 70 = 180 - 120 = 60°β = ∠А₁А₂В₂ = ∠А₂В₂С₂ = 50° как накрест лежащие

-
Автор:
deaconbrennan - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
В какой природной зоне расположен населённый пункт, в котором ты живёшь? Расскажи об особенностях животного мира, характерного для твоей местности.
Помоги пожалуйста ,буду очень благодарна! Если я живу в Екатеринбурге
-
Предмет:
Окружающий мир -
Автор:
frau fraummrv - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Какие выражения имеют одно и то же значение? Выпиши эти выражения и
поставь между ними знак равенства.
20-2; 28-8; 20+20; 4*5-
Предмет:
Математика -
Автор:
janetberger - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- Какова функция среднего мозга? Какова функция промежуточного мозга?
-
как животные помогают людям в поле
-
Предмет:
Окружающий мир -
Автор:
elsaknox - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
