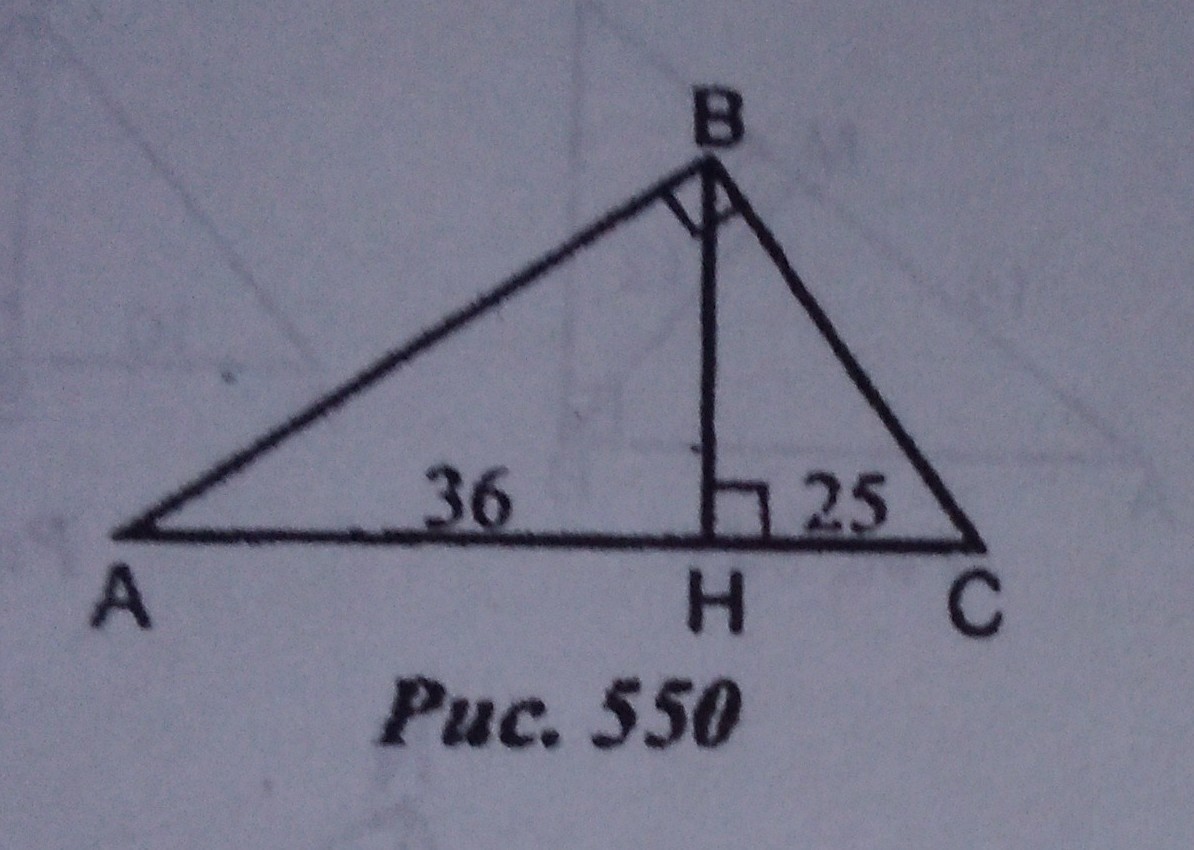
Помогите пожалуйста, надо найти а) BH, AB, BC. б) площадь ABH: площадь CBH

Тут та же история, что и в предыдущем задании, только данные другие.Высота, проведенная из вершины прямого угла, равна среднему геометрическому проекций катетов на гипотенузу: BН = √АН*СНАН=36, СН = 25, значит:ВН=√36*25ВН=√900=30Теперь у нас в обоих малых треугольниках известны оба катета. Ищем гипотенузы малых треугольников:АВ²=АН²+ВН²=1296+900=2196АВ=46,86ВС²=СН²=ВН²=625+900=1525ВС=39,05Проверим... АВ²+ВС² = АС²2196+1525=3721. Всё сходится...Ищем площади треугольников:Для АВН S=(AH*BH)/2 = (36*30)/2=540см²Для СВН S=(СН*ВН)/2 = (25*30)/=375см²