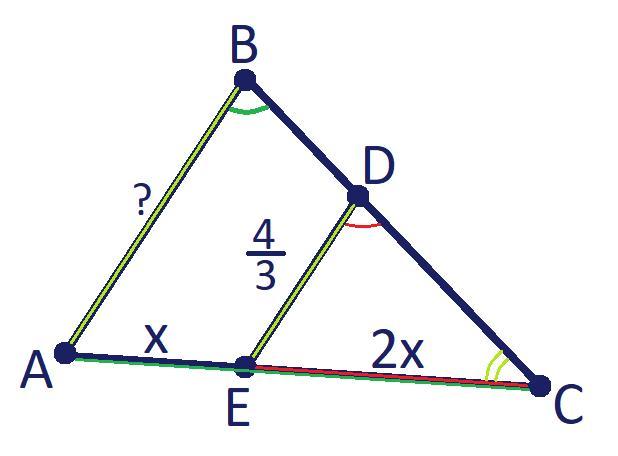
Точка E лежит на стороне AC треугольника ABC, причём EC/AE=2. Точка D лежит на BC, причём ED параллельна AB. Найти AB, если ED=4/3 (дробь).

Пусть AE = x, тогда по условию EC = 2·AE = 2x;

AC = AE+EC = x+2x = 3x.

∠CDE = ∠CBA, как соответственные углы при ED║AB и секущей BD;

△CED ~ △CAB по двум углам (∠ECD - общий; ∠CDE=∠CBA);

• В подобных треугольниках сходственные стороны пропорциональны и лежат против равных углов.

Из подобия треугольников получим следующею пропорцию:

\dfrac{EC}{AE} =\dfrac{ED}{AB} \Rightarrow AB=ED:\dfrac{EC}{AC};\\\\AB=ED\cdot \dfrac{AC}{EC} =\dfrac{4}{3} \cdot \dfrac{3x}{2x} =2

Ответ: 2.