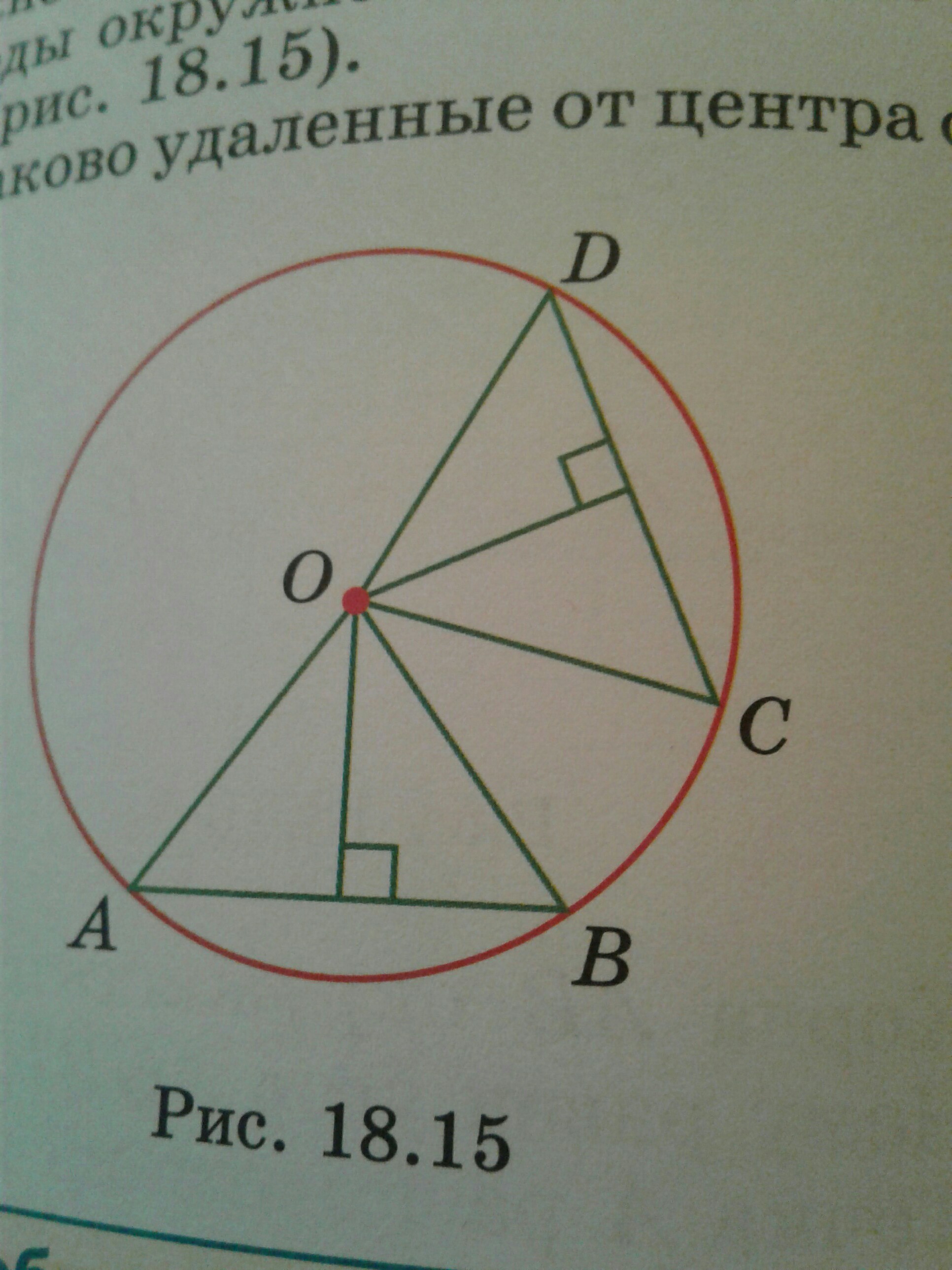
докажите, что хорды, одинаково удаленные от центра окружности равны рис.18.15

Пусть AB и CD - хорды, равноудаленные от центра О окружности. Тогда перпендикуляры, опущенные из центра на эти хорды будут равными (определяется как расстояние от точки до прямой). Доказательство:

1. Опустим из центра O окружности перпендикуляры OM и ON на хорды AB и CD соответственно. По условию OM = ON.
2. Так как OM и ON - радиусы, а хорды AB и CD являются диаметрами вписанных в окружность вписанных в неё треугольников, то AB = 2*AM и CD = 2*CN.
3. Поскольку OM = ON, следовательно, AM = CN (так как расстояния от точки до прямой равны).
4. Тогда AB = 2*AM = 2*CN = CD. Значит, хорды AB и CD равны.

Получаем, что хорды, перпендикулярно равноудаленные от центра окружности, равны. Это следует из свойства радиуса, перпендикулярного к хорде - он делит хорду пополам.