Касательная окружность , помогите пж

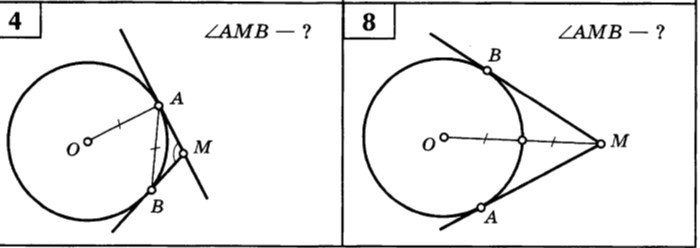
№4. Дано: Окр. О; AM - касательная, AM пересекает Окр. = А; BM - касательная, BM пересекает Окр. = B; OA = AB; Угол AMB - ? ---— Решение: Проведём радиус OB. OB = OA = AB, значит, треугольник OAB - равносторонний. Угол OAB равен углу ABO, равен углу BOA = 180°/3 = 60°. Т.к. AM - касательная, то угол OAM = 90°, значит, угол BAM = угол OAM - угол OAB = 90° - 60° = 30°. Аналогично, угол OBM равен 90°, угол ABM = 90° - 60° = 30°. По теореме о сумме углов треугольника, угол AMB = 180° - 30° - 30° = 120°. Ответ: угол AMB равен 120°. №8. Дано: Окр. О; BM и AM - касательные к Окр. из точки М; OM = 2r; Угол AMB - ? ---— Решение: Проведём радиусы OB и OA. Sin BMO = OB/OM; Т.к. OM = 2OB, то Sin BMO = 1/2, значит, угол BMO = 30°. Известно, что отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.Значит, угол BMO = углу OMA = 30°.Отсюда, угол AMB = угол BMO + угол OMA,Угол ABM = 30° + 30° = 60°.Ответ: угол ABM = 60°.