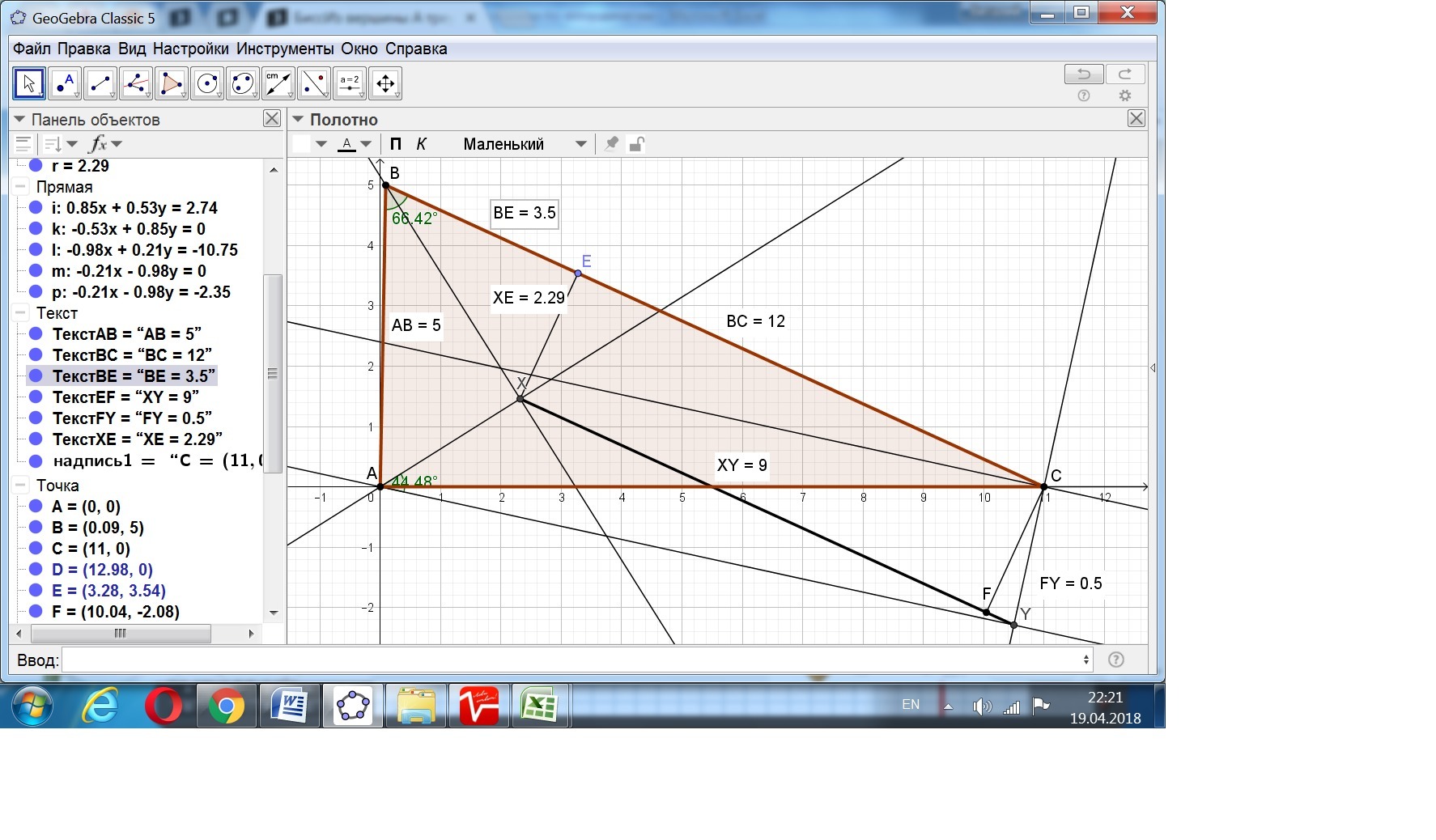
БиссИз вершины A треугольника ABC опущены перпендикуляр AX на биссектрису угла B и перпендикуляр AY на биссектрису внешнего угла C. Чему равна длина отрезка XY, если AB=5, AC=11, BC=12?

Даны длины сторон треугольника AB=5, AC=11, BC=12.Из вершины A треугольника ABC опущены перпендикуляр AX на биссектрису угла B и перпендикуляр AY на биссектрису внешнего угла C. Найти длину отрезка ХУ.Данную задачу можно решить двумя способами:1) геометрическим,2) векторным.1) По заданным длинам сторон треугольника АВС находим углы: cos A= (АВ²+АС²-ВС²)/(2*АВ*АС) = 0,018182. A = 1,552614 радиан = 88,9582 градусов. cos В= (АВ²+ВС²-АС²)/(2*АВ*ВС) = 0,4. B = 1,159279 радиан  = 66,42182 градусов. cos C= (АC²+ВС²-АВ²)/(2*АC*ВС) = 0,909091. C = 0,4297 радиан = 24,61998 градусов.Заданный отрезок ХУ рассмотрим как основание трапеции ВХУС.ХУ = 12 - 5*cos(B/2)*cos(B/2) + 5*cos(B/2)*sin(B/2)*tg(C/2).Подставив значения функций углов, находим: ХУ = 9.2) Рассмотрим треугольник АВС в системе координат: точка А - начало, точка С -на оси Ох.С учётом найденных значений углов, определяем координаты вершин: Точка А           Точка В                               Точка С Ха   Уа            Хв                 Ув                     Хс        Ус 0       0        0,090909     4,999173                 11         0 Используем формулу биссектрисы по координатам вершин и длинам сторон:  ВХ:  ((Уа-Ув + Ус-Ув )/АВ) * Х +  ((Хв-Ха + Хв-Хс )/ВС) * У + ((Ха*Ув - Хв*Уа)/АВ + (Хс*Ув - Хв*Ус)/ВС)  = 0.Подставив значения, получаем ВХ в виде уравнения с угловым коэффициентом:   у(ВХ) = -1,5898732 х + 5,143707.Уравнение перпендикуляра АХ из точки А на эту биссектрису с учётом к(АХ) = -1/к(ВХ) : у(АХ) =  0,628980978х.Находим координаты точки Х как точки пересечения прямых АХ и ВХ  x(Х) =  2,318182;  у(Х) = 1,4580923.Аналогично находим координаты точки У: x(У) = 10,5;  y(У) = -2,2912878.Теперь длина ХУ равна:ХУ = √((x(Х)-x(У))²+(у(Х)-у(У))²) = 9.