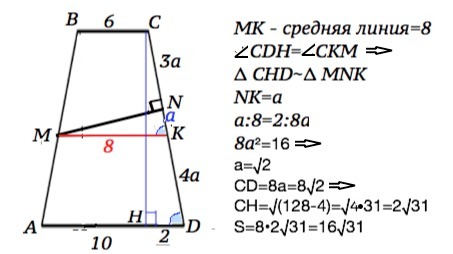
В равнобедренной трапеции ABCD с основаниями AD=10, BC=6 из середины M стороны AB опущен перпендикуляр MN на сторону CD. Известно, что CN:ND=3:5. Найти площадь трапеции ABCD.

Проведем отрезок МК║АD. Так как М - середина АВ, МК- средняя линия трапеции. МК=(6+10):2=8

Примем коэффициент отношения СN:ND равным а. 

Тогда СD=3a+5a=8a, 

CK=KD=8a:2=4a, из чего следует NK=a.

Опустим  высоту СН на АD. 

Высота, проведенная из тупого угла равнобедренной трапеции, делит большее основание на отрезки, один из которых равен полуразности оснований, другой – их полусумме. => 

DH=(10-6):2=2,  AH=MN=(10+6):2=8

МК║AD, СD – секущая =>  ∠CKM=∠CDA. 

Прямоугольные ∆ СDH~∆ MKN по острому углу.

Из подобия следует: Отношение катетов к гипотенузе подобных прямоугольных треугольников равно. 

NK:MK=HD:СD

a:8=2:8a 

8a²=16  =>

a=√2 и СD=8√2

По т.Пифагора 

CH=√(CD²-HD²)=√(128-4)=2√31

Площадь трапеции равна произведению высоты на полусумму оснований:

S=(2√31)•8=16√31 (ед. площади)