Решите, пожалуйста! Даю много баллов, так как срочно.

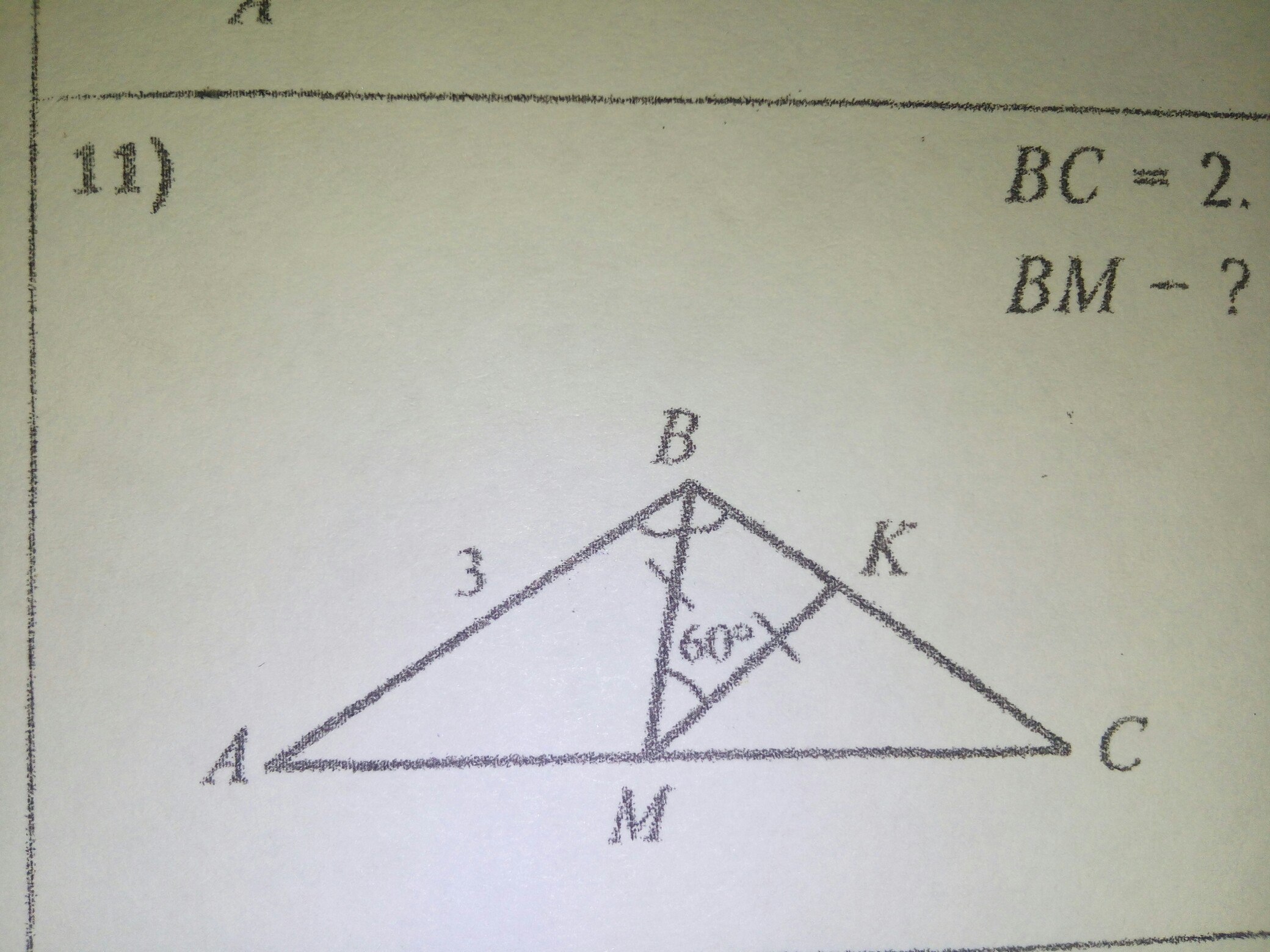
На рисунке треугольник ВМК равнобедренный, угол ВМК=60°, поэтому углы при его основании ВК также равны 60°. 

Указано равенство ∠АВМ и ∠СВМ. 

Следовательно, ВМ биссектриса,  ∠НВМ=60°, ⇒ ∠АВС=120° 

Проведем высоту СТ к стороне АВ. 

Высота из вершины острого угла тупоугольного треугольника находится вне треугольника и пересекает продолжение стороны. 

∆ СВТ прямоугольный с углом СВТ=60° ( смежный углу АВС).  

ТС=ВС•sin60°=2:√3/2=√3

Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон => 

АМ:МС=АВ:ВС=3/2

АС=АМ+МС= 3+2=5 частей. 

Проведем МН║СТ

Прямоугольные ∆ АТС и АНМ подобны по общему острому углу А. 

 k=АМ:АС=3/5

НМ=ТС•3/5=(√3)•3/5

BM=HM:sin60°=6/5=1,2  (ед. длины)

Есть формулы для нахождения биссектрисы произвольного треугольника. Для данной задачи подойдет формула 

, где L - биссектриса, а и b- стороны треугольника, α - угол между ними. Вычисления дают длину ВМ=1,2