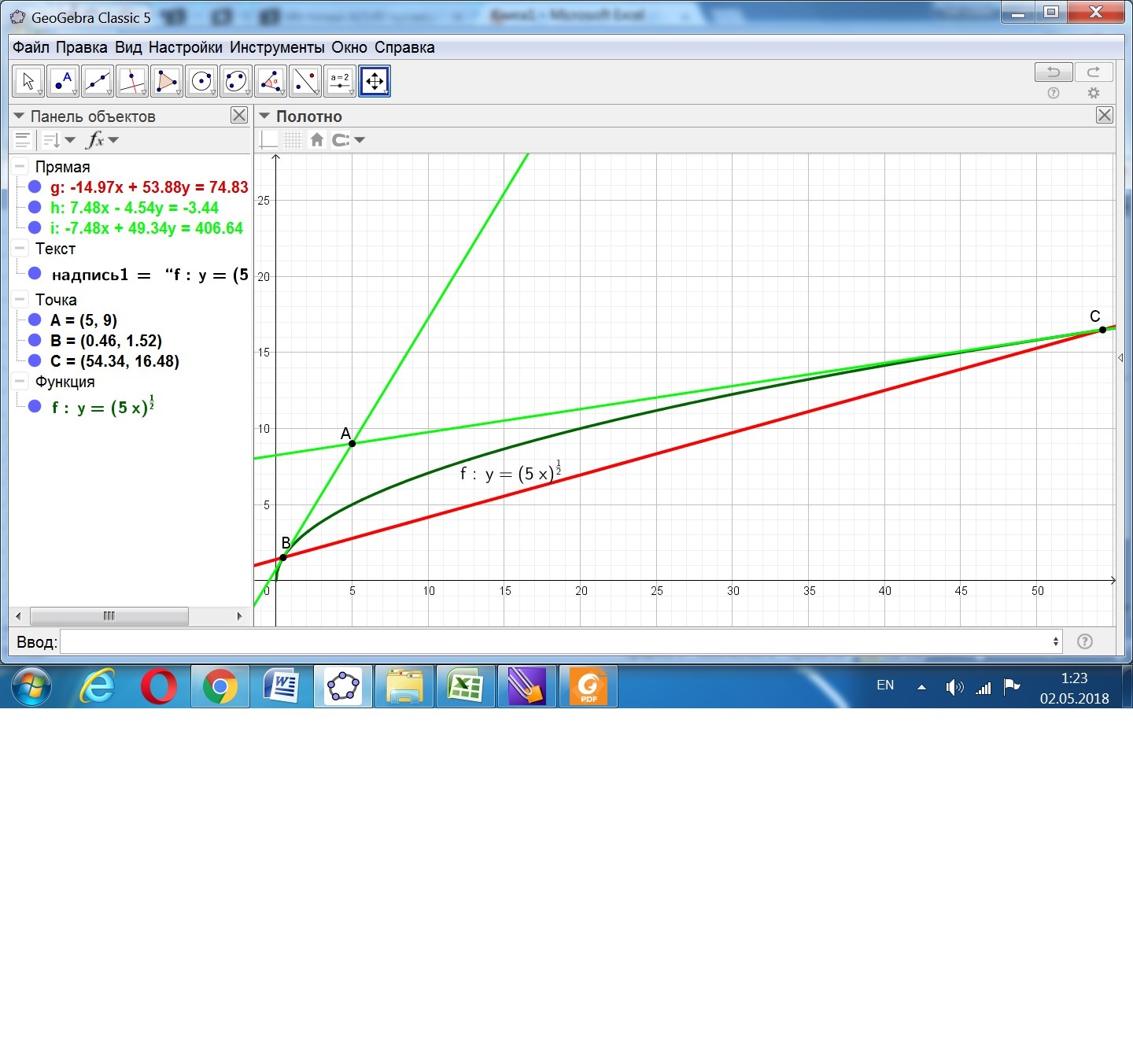
Из точки А(5;9) проведены касательные к параболе y^2=5x. Составить уравнение хорды, соединяющей точки касания.

Даны парабола у² = 5х и точка А(5;9).Находим уравнения касательных к заданной параболе, проходящих через точку А.y' = √5/(2√x),   y/(xo) = √5/(2√xo).yкас = (√5/(2√xo))*(x - xo) + (√(5xo)).Так как касательные проходят через точку А, подставим её координаты вместо переменных х и у:9= \frac{ \sqrt{x} }{2 \sqrt{xo} } (5-xo)+ \sqrt{5xo} .Решением этого уравнения есть 2 точки касания:х₁ = (137/5)-(36√14/5) ≈ 0,46006682.у₁ = √(137 - 36√14) ≈ 1,516685.х₂ =  (137/5)+(36√14/5) ≈ 54,33993.у₂ = √(137 + 36√14) ≈ 16,48331.Общее уравнение прямой, проходящей через точки касания, с точностью до двух знаков:  -14,97х + 53,88у = 74,83.Для получения уравнения в каноническом виде (х - хВ)/(хС - хВ) = (у - уВ)/(уС - уВ) надо подставить координаты точек касания.