На стороне BC параллелограмма ABCD отмечены точки M так, что BM: MC = 1: 3. Почему равны площадь треугольника ABM, если площадь параллелограмма равны S? Помогите пожалуйста, (

На стороне ВС параллелограмма ABCD отмечена такая точка М, что ВМ : МС = 1 : 3. Чему равна площадь треугольника АВМ, если площадь параллелограмма равна S?

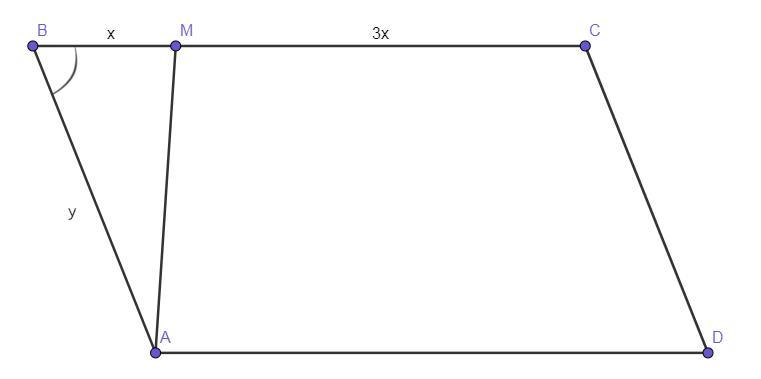
Чертёж смотрите во вложении.

Дано:

Четырёхугольник ABCD - параллелограмм.

Точка М ∈ ВС.

ВМ : МС = 1 : 3.

S(ABCD) - S.

Найти:

S(ΔАВМ) = ?

Решение:

Пусть ВМ = х, тогда МС = 3х, АВ = у. Площадь ΔАВМ обозначим как S₁.

Площадь параллелограмма равна произведению смежных сторон и синусу угла между ними.

Следовательно -

S(ABCD) = ВС*АВ*sin (∠В)

ВС = ВМ+МС = х+3х = 4х.

То есть -

S = 4ху*sin (∠В)

Рассмотрим ΔАВМ.

Площадь треугольника равна половине произведения смежных сторон и синуса угла меду ними.

То есть -

S(ΔАВМ) = 0,5*ВМ*АВ*sin (∠В)

S₁ = 0,5*хy*sin (∠В).

\left \{ {{S_{1}= 0,5*xy*sin (B)} \atop{ S = 4xy*sin (B)}} \right. \\

Из первого уравнения системы следует, что -

xy = \frac{S_{1} }{0,5*sin (B)}

Подставим это значения во второе уравнение системы -

S = 4*\frac{S_{1} }{0,5*sin(B)} *sin (B)}}\\\\S=4*\frac{S_{1} }{0,5} \\\\S=8*S_{1} \\\\ S_{1} =\frac{S}{8}

S(ΔАВМ) = S(ABCD)/8

S(ΔАВМ) = S/8.

Ответ: S/8.