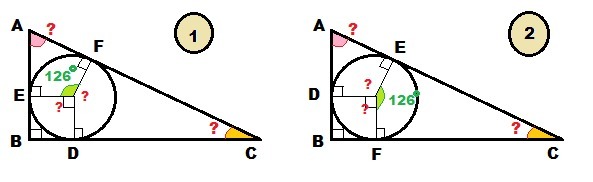
В прямоугольный треугольник ABC вписана окружность, угол B — прямой. Вычисли углы треугольника A и C, а также центральные углы, если ∢EOF=126°. ∢A= ° ∢C= ° ∢DOE= ° ∢FOD= °

В условии ничего не сказано, где расположены точки E, F, D.Так как в треугольник вписана окружность, можно предположить, что E, F, D - точки касания. Тогда возможно 4 варианта расположения точек с учётом угла ∠EOF = 126° Для решения нужно знать:Радиус в точку касания образует прямой угол с касательной.Сумма острых углов прямоугольного треугольника равна 90°Сумма углов любого четырёхугольника равна 360°1) Точки E и D - точки касания катетов, F - точка касания гипотенузыЧетырёхугольник AFOE :∠A = 360°-∠EOF -∠AEO -∠AFO = 360°-126°-90°-90° = 54°ΔABC - прямоугольный, ∠B = 90°, ∠A = 54°∠С = 90° - ∠A = 90° - 54° = 36°BEOD - квадрат ⇒ ∠DOE = 90°Четырёхугольник CFOD :∠FOD = 360° -∠CFO -∠CDO -∠C = 360°-90°-90°-36° = 144°2) Точки F и D - точки касания катетов, E - точка касания гипотенузыЧетырёхугольник CFOE :∠C = 360°-∠EOF -∠CEO -∠CFO = 360°-126°-90°-90° = 54°ΔABC - прямоугольный, ∠B = 90°, ∠C = 54°∠A = 90° - ∠C = 90° - 54° = 36°BFOD - квадрат ⇒ ∠DOF = 90°Четырёхугольник AEOD :∠EOD = 360° -∠AEO -∠ADO -∠A = 360°-90°-90°-36° = 144°Как видно из решения, меняются обозначения точек, но величины углов получаются одинаковыми. Такими же они и останутся для вариантов 3 и 4, если обозначение точек касания катетов поменять местами.Ответ независимо от буквенного обозначения:острые углы будут равны 54° и 36°,центральные углы будут равны  126°, 90°, 144°