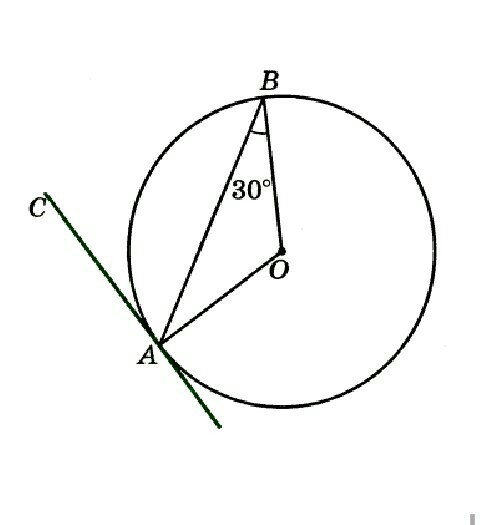
CA касательная к окружности. Вычислите градусную меру угла BAC.

Дано:

Окружность (О; r)

∠OBA = 30°

CA — касательная

Найти:

∠BAC — ?

Решение:

1) Так как радиусы окружности равны, значит, две стороны треугольника ABO равны. ⇒ ΔABO равнобедренный (AO = OB).

У равнобедренного треугольника углы при основании равны, следовательно: ∠OBA = ∠OAB = 30°.

2) Касательная к окружности перпендикулярна радиусу, проведённому в точку касания, значит CA ⊥ OA. ∠OAC = 90°.

3) ∠BAC = ∠OAC - ∠OAB.

∠BAC = 90° - 30° = 60°.

ОТВЕТ: 60°

___________________

Быстрое решение (пояснения писать обязательно нужно):

1) ΔABO равнобедренный, так как радиусы окружности, составляющие стороны треугольника, равны (AO = OB). Следовательно, ∠OBA = ∠OAB = 30°.

По свойству касательной, CA ⊥ OA ⇒ ∠OAC = 90°. Значит:

2) ∠BAC = 90° - 30° = 60°

ОТВЕТ: 60°