-
5.Один из соответственных углов, образованных при пересечении прямых
n и m, секущей k, больше другого. Определите взаимное расположение прямых n и m.
а) пересекаются б) параллельны в) такая ситуация невозможна.
6. В прямоугольном треугольнике один из острых углов равен 35°. Чему равен второй острый угол?
а) 35° б) 55° в) 145° в) 90°
7. Углы треугольника относятся как 1:1:1. Определите вид данного треугольника.
по углам: по сторонам:
а) остроугольный а) разносторонний
б) прямоугольный б) равносторонний
в) тупоугольный в) равнобедренный
8. Треугольника, с такими сторонами не существует:
а) 4;5;6; б) 5;5;6; в) 8; 4;3; г) 12; 21; 15
9. Выберите верное утверждение.
а) Через любые две точки проходит прямая, и притом только одна
б) Градусная мера острого угла больше 90º
в) При параллельных прямых и секущей накрест лежащие углы в сумме образуют 180º
г) Два треугольника равны, если соответствующие углы равны
Ответы 1
-
Проанализируем каждое задание.
5. Если при пересечении двух прямых секущей соответственные углы имеют разные градусные меры, то такие прямые пересекаются на плоскости.
Ответ: а) пересекаются.6. Сумма острых углов прямоугольного треугольника равна 90°. Первый острый угол = 35°, следовательно, второй острый угол = 90°-35° = 55°.
Ответ: б) 55°.7. Если углы треугольника пропорциональны числам 1:1:1, то пусть каждый из этих углов этого треугольника равен х, х, х. Сумма углов треугольника равна 180°.
Составим уравнение и решим его -
х+х+х = 180°
3х = 180°
х = 60°
Каждый из углов треугольника равен по 60°. А если все углы треугольника равны по 60°, то такой треугольник является равносторонним (вид треугольника по сторонам). Равносторонний треугольник всегда является остроугольным, так как все углы острые (вид треугольника по углам).
Ответ: а) остроугольный, б) равносторонний.8. Каждая сторона треугольника меньше суммы двух других сторон. Составляем неравенства и проверяем их на верность.
а) 4+5 > 6 - верное неравенство.
6+5 > 4 - верное неравенство.
4+6 > 5 - верное неравенство.
Такой треугольник существует.
б) 5+5 > 6 - верное неравенство.
5+6 > 5 - верное неравенство.
5+6 > 5 - верное неравенство.
Такой треугольник существует.
в) 4+8 > 3 - верное неравенство.
4+3 > 8 - неверное неравенство.
Такого треугольника не существует.
г) 12+21 > 15 - верное неравенство.
12+15 > 21 - верное неравенство.
15+21 > 12 - верное неравенство.
Такой треугольник существует.
Ответ: в) 8; 4; 3.9) Проанализируем каждое утверждение.
а) Верно, это аксиома планиметрии.
б) Неверно. Острый угол всегда меньше 90° (к тому же не может принимать значение в 0°).
в) Неверно. В сумме накрест лежащие углы, конечно же, могут давать 180°. Но это в том случае, когда секущая перпендикулярна параллельным прямым. А ведь секущая не всегда может их пересекать под прямым углом.
г) Неверно. Такие треугольники подобны. Чтобы доказать равенство таких треугольников нужна хотя бы ещё равная сторона.
Ответ: а) Через любые две точки проходит прямая, и притом только одна.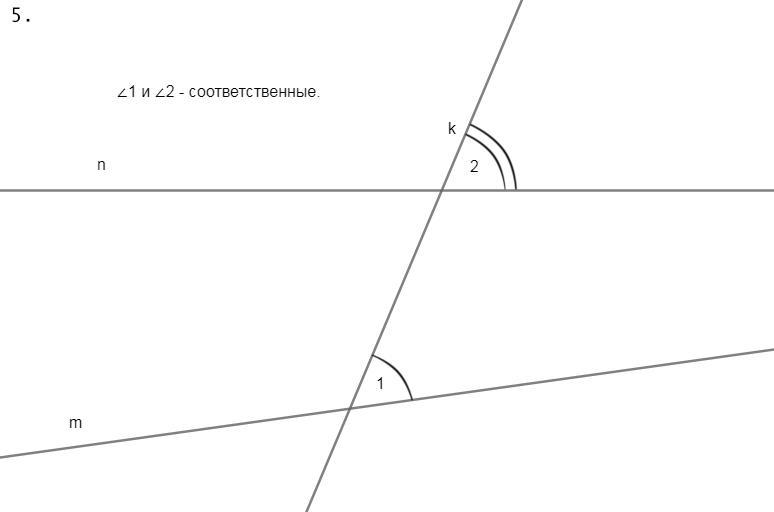

-
Автор:
t-birdanjy - 2 года назад
-
0
-
-
Добавить свой ответ
-
два стоелка стреляют по мишени. первый попадает в мишень с вероятностью 0.7, а второй - с вероятностью 0.8. какова вероятность того, что а) оба не попадут; б) хотя бы один попадет
-
Предмет:
Математика -
Автор:
calebwright - 6 лет назад
-
Ответов:
5 -
Смотреть
-
- условие равномерно прямолинейного движения
-
Почему битва при каннах вошла в историю
-
План выхожу в космос
-
Предмет:
Литература -
Автор:
fiestakgig - 6 лет назад
-
Ответов:
1 -
Смотреть
-
