-
Нужна задача только №5
Дано: прямая CD перпендикулярная плоскости ADB, ∠ADB = 90°.
Найти угол между плоскостями ACB и ADC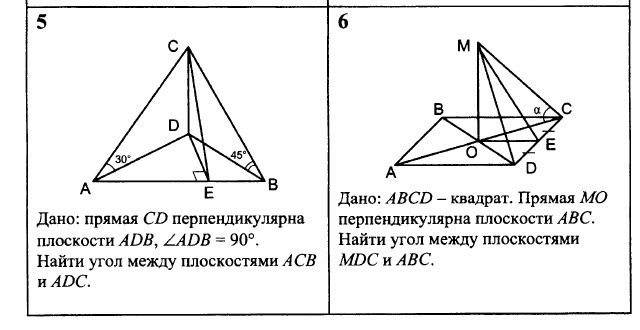
Ответы 1
-
Дано: прямая СD перпендикулярна плоскости ADB, <ADB=90°. Найти угол между плоскостями АСВ и ADC.
* * *
Ответ: arctg (√6)/3
Объяснение: Угол между плоскостями – двугранный угол. Его величина определяется градусной мерой линейного угла, сторонами которого являются лучи, проведённые в его гранях перпендикулярно ребру с общим началом на нём.
Наклонная СЕ⊥АВ, по т. о 3-х перпендикулярах её проекция DE⊥АВ, ⇒ ∠СЕD - искомый.
Примем СD=a, тогда АD=CD•ctg30°=a√3; Треугольник CDB прямоугольный равнобедренный ( т.к. острый угол=45°) ⇒ ВD=CD=a.
В ∆ АDB высота DE=AD•DB:AB
AB=√(AD²+BD²)=√(3a²+a²)=2a ⇒
DE=a√3•a√2:2a=(a√6)/2 ⇒
tgCED=a:(a√6)/2=(√6)/3
∠CED=arctg (√6)/3 – это угол ≈39°14'
-
Автор:
lizbethramsey - 6 лет назад
-
0
-
-
Добавить свой ответ
-
твір?) есе на тему (що таке доброта ?)
-
Предмет:
Українська мова -
Автор:
diana37 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Сочинить короткий рассказ о папе ёжика и ежонка
-
Предмет:
Литература -
Автор:
eliseodixon - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В цеху работают токари, слесари и фрезеровщики. Число слесарей равно числу токарей и в 2 раза больше числа фрезеровщиков. Какое из следующих чисел 32, 28, 25, 24, 42 может быть числом всех рабочих, работающих в этом цеху
-
Предмет:
Математика -
Автор:
weston - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Составьте слово из заданных гласных букв, согласные буквы используйте любые.
1) о, о, о, и
2) о, е, и, е
3) о, а, о, о-
Предмет:
Биология -
Автор:
alenavance - 6 лет назад
-
Ответов:
1 -
Смотреть
-
