помогите, надо найти площадь полной поверхности

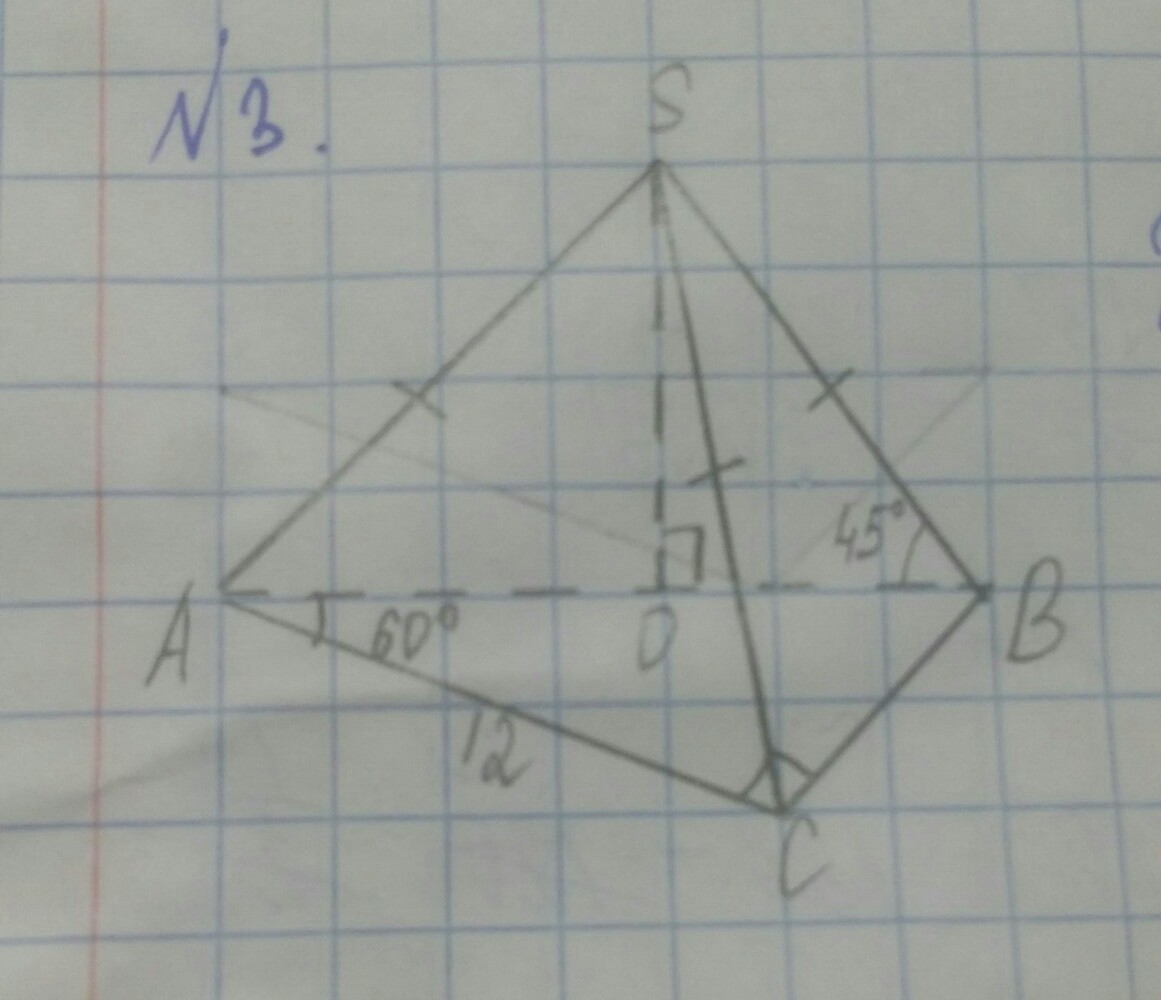
Треугольник ∴ АВС:     <C=90°;   <B=90° - 60°=30°;   катет АС=12  ;                           гипотенуза АВ=12*2=24;                            катет   СВ=√(24²-12²)=√(12²*2²-12²)= 12√3S(ABC)=(12*12√3)/2=6*12√3Треугольник ∴ASB :   AB=24;  т.к. AS=SB, то <B=<A=45°;                         <S=180-45-45=90°;   <OSD=45°;                                                                       AD=DB=DS=AB/2=24/2=12S(ASB)=12*12/2=6*12;          SB=√(DB²+SD²)=√(12²+12²)=12√2Треугольник  ∴SCB:    SC=SB=12√2     CB=12√3       h=√(SB)²-(CB/2)² =√(12² *2-12² *3/4) =12√(2-3/4)=12√(4/4-3/4)=12/2=6S(SCB)=(6*12√3)/2=3*12√3Треугольник ∴ASC:    AS=SC=12√3    AC=12         h=√(AS²-(AC/2)²)=√(12² *3 - 12²/2²)=12√(3-1/4)=12√(11/4)=6√11S(ASC)=(AC/2  *h)/2= (6*6√11 )/2=18√11Вся площадь=6*12√3+6*12+3*12√3+18√11=12*(6√3+1+3√3)+18√11==12*(9√3+1)+18√11   <---- ответ